Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
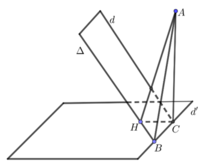
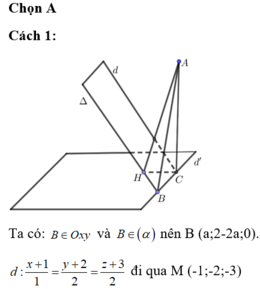
Cách 1: Ta có: B ∈ Oxy và B ∈ (α) nên B (a ; 2 – 2a ; 0).
![]() đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là
đi qua M (-1 ; -2 ; -3) và có một véctơ chỉ phương là ![]()
Ta có: d ⊂ (α) nên d và Δ song song với nhau và cùng nằm trong mặt phẳng (α).
Gọi C = d ∩ (Oxy) nên 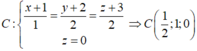
Gọi d’ = (α) ∩ (Oxy), suy ra d’ thỏa hệ 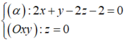
Do đó, d’ qua 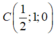 và có VTCP
và có VTCP ![]()
Gọi φ = (Δ, d’) = (d, d’)
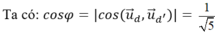
Gọi H là hình chiếu của C lên Δ. Ta có CH = 3 và 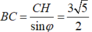
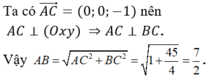
Cách 2: Ta có: ![]() đi qua M (-1 ; -2 ; -3) và có một VTCP là
đi qua M (-1 ; -2 ; -3) và có một VTCP là ![]()
Ta có: B = Δ ∩ (Oxy), Δ ⊂ (α) nên B ∈ (Oxy) ∩ (α) => B (a; 2 – a; 0)
Ta có: Δ // d và d (Δ, d) = 3 nên 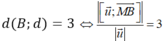
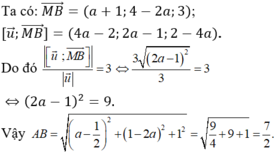

Ta có: d ⊂ (α) nên d và ∆ song song với nhau và cùng nằm trong mặt phẳng (α).
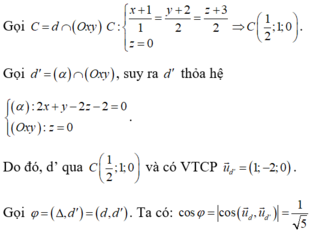


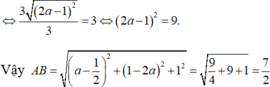

Chọn B
Phương trình (S): x2 + y2 + z2 + 4x - 6y + m = 0 là phương trình mặt cầu <=> m < 13
Khi đó (S) có tọa độ tâm I (-2;3;0) bán kính ![]()
Gọi M (x;y;z) là điểm bất kỳ thuộc Δ.
Tọa độ M thỏa mãn hệ: 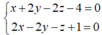
Đặt y = t ta có: 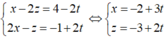
=> Δ có phương trình tham số: 
Δ đi qua điểm N (-2; 0; -3) và có vectơ chỉ phương ![]()
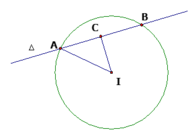
Giả sử mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8. Gọi (C) là đường tròn lớn chứa đường thẳng Δ. Khi đó IC2 = R2 - AC2 = 13 - m - 42 = -m - 3
N (0;-3;-3)

Vậy mặt cầu (S) cắt Δ tại hai điểm phân biệt A, B sao cho AB = 8
<=> -m - 3 = 9 <=> m = -12

Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng

Chọn D
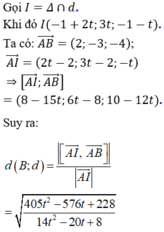
Xét hàm số:
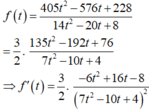
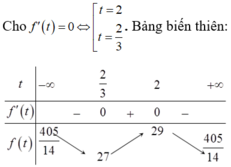
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()

Đáp án A
Ta có: phương trình hoành độ giao điểm của (C) và ![]() (x ≠ 0).
(x ≠ 0).
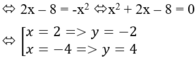
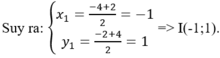
Gọi I(x1;y1) là trung điểm đoạn thẳng AB.



a) Xét ΔAMB và ΔAMC: AB=AC
\(\widehat{BAM}=\widehat{MAC}\) (AM là phân giác Â)
AM: chung
⇒ ΔAMB = ΔAMC (c.g.c)
b) Vì ΔAMB=ΔAMC (cmtrn)
⇒ BM=MC (2 cạnh tương ứng)
⇒ \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
mà \(\widehat{AMB}+\widehat{BMD}= \widehat{AMC}+\widehat{DMC}\) ( 2 góc kề bù)
\(180^0\) = \(180^0\)
⇒ \(\widehat{BMD}=\widehat{DMC}\)
Xét ΔMBD và ΔMCD :
BM=MC (cmtrn)
\(\widehat{BMD}=\widehat{DMC}\) (cmtrn)
MD: chung
⇒ ΔMBD = ΔMCD (c.g.c)