Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha
c. Chứng minh D, K, E thẳng hàng.
Ta có: ^EBK + ^ABK = 180 độ (2 góc kề bù)
^CDK + ^ADK = 180 độ (2 góc kề bù)
^ABK = ^ADK (tam giác ABK = tam giác ADK)
=> ^EBK = ^CDK
Xét tam giác EBK và tam giác CDK ta có:
EB = CD (gt)
^EBK = ^CDK (cmt)
BK = DK (tam giác ABK = tam giác ADK)
=> tam giác EBK = tam giác CDK (c - g - c)
=> ^EKB = ^CKD (2 góc tương ứng)
Mà 2 góc này ở vị trí đối đỉnh
Nên D, E, K thẳng hàng

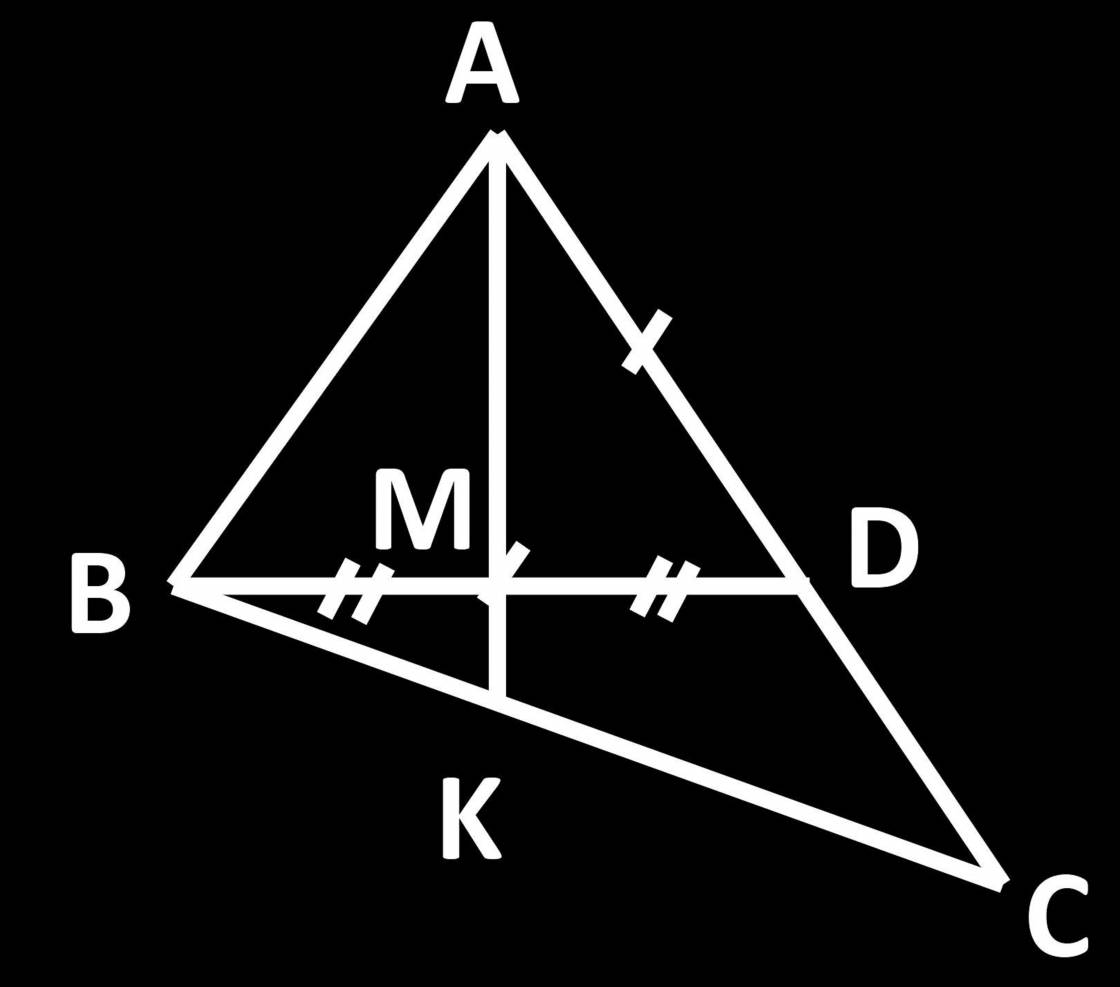
Xét ΔABD có AB=AD
nên ΔABD cân tại A
Ta có: ΔABD cân tại A
mà AK là đường trung tuyến
nên AK là phân giác của góc BAD
Xét ΔABK và ΔADK có
AB=AD
\(\widehat{BAK}=\widehat{DAK}\)
AK chung
Do đó: ΔABK=ΔADK
=>KB=KD

Giải:
a) Xét \(\Delta ABM,\Delta ADM\) có:
\(AB=AD\left(gt\right)\)
\(\widehat{ABM}=\widehat{ADM}\) ( do \(\Delta ABD\) cân tại A vì AB = AD )
\(BM=MD\left(=\frac{1}{2}BD\right)\)
\(\Rightarrow\Delta ABM=\Delta ADM\left(c-g-c\right)\)
b) Vì \(\Delta ABM=\Delta ADM\)
\(\Rightarrow\widehat{A_1}=\widehat{A_2}\) ( cạnh t/ứng )
Xét \(\Delta ABK,\Delta ADK\) có:
\(AB=AD\left(gt\right)\)
\(\widehat{A_1}=\widehat{A_2}\) ( cmt )
\(AK\): cạnh chung
\(\Rightarrow\Delta ABK=\Delta ADK\left(c-g-c\right)\)
Vậy...
Hoàng ơi, nếu có bài gì khó, bạn cứ mang lên hỏi các bạn lớp mình. Mà nếu các bạn ấy ko giảng cho bạn, thì bạn bảo tôi nhé ! Có lẽ sẽ có một số bài tôi ko làm được ! Nhưng tôi sẽ nhiệt tình giúp bạn ! Bạn ko cần lên đây hỏi nữa, Hoàng nhé !

c) Δ ABK = Δ ADK (câu b) => BK = DK (2 cạnh tương ứng)
và ABK = ADK (2 góc tương ứng)
Mà ABK + KBE = 180o (kề bù)
ADK + KDC = 180o (kề bù)
nên KBE = KDC
Xét Δ KBE và Δ KDC có:
BE = CD (gt)
KBE = KDC (cmt)
BK = DK (cmt)
Do đó, Δ KBE = Δ KDC (c.g.c)
=> BKE = DKC (2 góc tương ứng)
Lại có: BKD + DKC = 180o (kề bù)
Do đó, BKE + BKD = 180o
=> EKD = 180o
hay 3 điểm E, K, D thẳng hàng (đpcm)
Silver bulletsoyeon_Tiểubàng giảiPhương AnNguyễn Huy TúHoàng Lê Bảo NgọcTrương Hồng Hạnh giải giúp mk bài hình đó đi![]()

a Xét ΔABM và ΔADM có
AB=AD
AM chung
BM=DM
Do đó: ΔABM=ΔADM
b: Ta có: ΔABD cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔABK và ΔADK có
AB=AD
\(\widehat{BAK}=\widehat{DAK}\)
AK chung
Do đó: ΔABK=ΔADK
Suy ra: KB=KD