Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(M\left(x\right)=-x^2+5\)
Có \(-x^2\le0\forall x\)
=> \(M\left(x\right)\le5\forall x\)
=> M(x) không có nghiệm.
2/
Thay \(x=\dfrac{1}{2}\) vào đa thức M(x) có
\(M\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\)
\(\Leftrightarrow a=2\)
Vậy...

`a, A(x) = 2x^3 + x - 3x^2 - 2x^3 - 1 + 3x^2`
`= (2x^3-2x^3) +(-3x^2+ 3x^2) + x-1`
`= x-1`
Bậc của đa thức : `1`
`b,` Ta có ` A(x)= x-1=0`
`x-1=0`
`=>x=0+1`
`=>x=1`
a) \(A\left(x\right)=2x^3+x-3x^2-2x^3-1+3x^2\)
\(A\left(x\right)=\left(2x^3-2x^3\right)-\left(3x^2-3x^2\right)+x-1\)
\(A\left(x\right)=x-1\)
Đa thức có bật 1
b) \(x-1=0\)
\(\Rightarrow x=1\)
Vậy đa thức có nghiệm là 1

a) \(f\left(x\right)=x^2-\left(m-1\right)x+3m-2\)
Để đa thức f(x) có nghiệm là -1 khi:
\(f\left(-1\right)=\left(-1\right)^2-\left(m-1\right).\left(-1\right)+3m-2=0\)
\(\Rightarrow1+m-1+3m-2=0\)
\(\Rightarrow4m=2\Rightarrow m=\dfrac{1}{2}\)
b) \(g\left(x\right)=x^2-2\left(m+1\right)x-5m+1\)
Để đa thức g(x) có nghiệm là 2 khi:
\(g\left(2\right)=2^2-2\left(m+1\right).2-5m+1=0\)
\(\Rightarrow4-4\left(m+1\right)-5m+1=0\)
\(\Rightarrow4-4m-1-5m+1=0\)
\(\Rightarrow-9m=-4\Rightarrow m=\dfrac{4}{9}\)
c) \(h\left(x\right)=-2x^2+mx-7m+3\)
Để đa thức h(x) có nghiệm là -1 khi:
\(h\left(-1\right)=-2\left(-1\right)^2+m.\left(-1\right)-7m+3=0\)
\(\Rightarrow-2-m-7m+3=0\)
\(\Rightarrow-8m=-1\Rightarrow m=\dfrac{1}{8}\)
d) -Để \(f\left(1\right)=g\left(2\right)\) khi và chỉ khi
\(1^2-\left(m-1\right).1+3m-2=2^2-2\left(m+1\right).2-5m+1\)
\(\Rightarrow1-m+1+3m-2=4-4m-4-5m+1\)
\(\Rightarrow11m=1\Rightarrow m=\dfrac{1}{11}\)
-Để \(g\left(1\right)=h\left(-2\right)\) khi và chỉ khi
\(1^2-2\left(m+1\right).1-5m+1=-2\left(-2\right)^2+m.\left(-2\right)-7m+3\)
\(\Rightarrow1-2m-2-5m+1=-8-2m-7m+3\)
\(\Rightarrow2m=-5\Rightarrow m=-\dfrac{5}{2}\)

a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
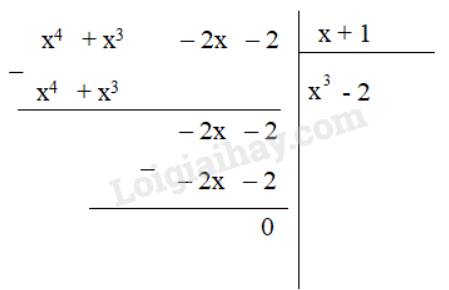
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
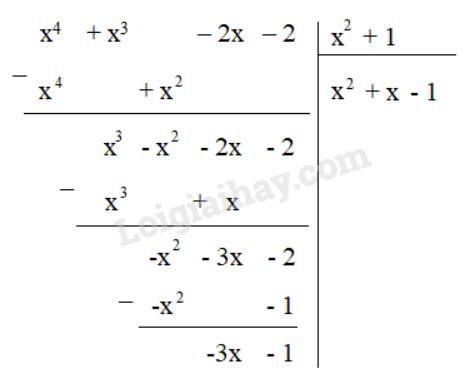
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn

2) Vì x=-1 là nghiệm của đa thức P(x)
=>P(-1)= m\(^2\)(-1)+16 =0
m\(^2\)(-1) = 0-16
m\(^2\)(-1) = -16
m\(^2\) = (-16):(-1)
m\(^2\) = 16
=> m = \(\sqrt{16}\)
=> m= 4 hoặc m= -4
=>Giá trị của m=4 hoặc m=-4
thay x=-1 vào đa thức F(x) ta có :
F(-1)=2.a.(-1)\(^2\)+b.(-1)=0
2.a.1+b.(-1)=0
2.a-b =0
2a=0+b
=>2a=b
ta có M=\(\dfrac{a+b+5}{6a+10}\)
=\(\dfrac{a+2a+5}{6a+10}\)
=\(\dfrac{3a+5}{2\left(3a+5\right)}\)
=\(\dfrac{1}{2}\)

A(x) = (2a-1)x\(^2\) - (3-4a)x + 1 - 6a
Thay x=\(\frac{-1}{2}\)vào A, có:
(2a-1)(\(\frac{-1}{2}\))\(^2\) - (3-4a)(\(\frac{-1}{2}\)) + 1 - 6a=0 <=>(2a-1)\(\frac{1}{4}\)+(3-4a)\(\frac{1}{2}\)+1-6a=0 <=> \(\frac{a}{2}\)- \(\frac{1}{4}\)+\(\frac{3}{2}\) - 2a +1 - 6a=0<=> \(\frac{2a}{4}\)-\(\frac{1}{4}\)+\(\frac{6}{4}\)-\(\frac{8a}{4}\)+ \(\frac{4}{4}\)- \(\frac{24a}{4}\)=0 <=>\(\frac{2a-1+6-8a+4-24a}{4}\)=0 => 2a -1 + 6 - 8a + 4- 24a=0 <=> 9-30a=0 <=> 30a =9
<=> a =\(\frac{9}{30}\)=\(\frac{3}{10}\) Vậy phườn trình có tập nghiệm S={\(\frac{3}{10}\)}
Thay \(x=\frac{-1}{2}\) vào đa thức \(A\left(x\right)=\left(2a-1\right)x^2-\left(3-4a\right)x+1-6a\), ta được:
\(A\left(-\frac{1}{2}\right)=\left(2a-1\right)\cdot\left(-\frac{1}{2}\right)^2-\left(3-4a\right)\cdot\frac{-1}{2}+1-6a\)
\(=\left(2a-1\right)\cdot\frac{1}{4}+\left(4a-3\right)\cdot\frac{-1}{2}+1-6a\)
\(=\frac{1}{2}a-\frac{1}{4}-2a+\frac{3}{2}+1-6a\)
\(=\frac{-15}{2}a+\frac{9}{4}\)
Để đa thức \(A\left(x\right)=\left(2a-1\right)x^2-\left(3-4a\right)x+1-6a\) nhận \(-\frac{1}{2}\) là nghiệm thì \(A\left(\frac{-1}{2}\right)=0\)
⇔\(\frac{-15}{2}a+\frac{9}{4}=0\)
\(\Leftrightarrow\frac{-15}{2}a=\frac{-9}{4}\)
⇔\(a=\frac{-9}{4}:\frac{-15}{2}=\frac{-9}{4}\cdot\frac{2}{-15}=\frac{3}{10}\)
Vậy: Khi \(a=\frac{3}{10}\) thì đa thức \(A\left(x\right)=\left(2a-1\right)x^2-\left(3-4a\right)x+1-6a\) nhận \(-\frac{1}{2}\) là nghiệm