Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ x8+x4y4+y8=(x4+y4)2-x4y4=(x4+y4-x2y2) (x4+y4+x2y2)=4(x4+y4-x2y2) =8
=>(x4+y4-x2y2)=2=>x4+y4=2+x2y2 kết hợp với x4+y4+x2y2=4
=> 2+x2y2+x2y2=4 => x2y2=1 (x4y4 sẽ = 1 nốt ) => x4+y4=3 và x8+y8=7
Xét (x4+y4)3=x12+y12+3x4y4(x4+y4)=x12+y12+3.1.3=33=27
=>x12+y12=18=> A = 18+1=19

a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
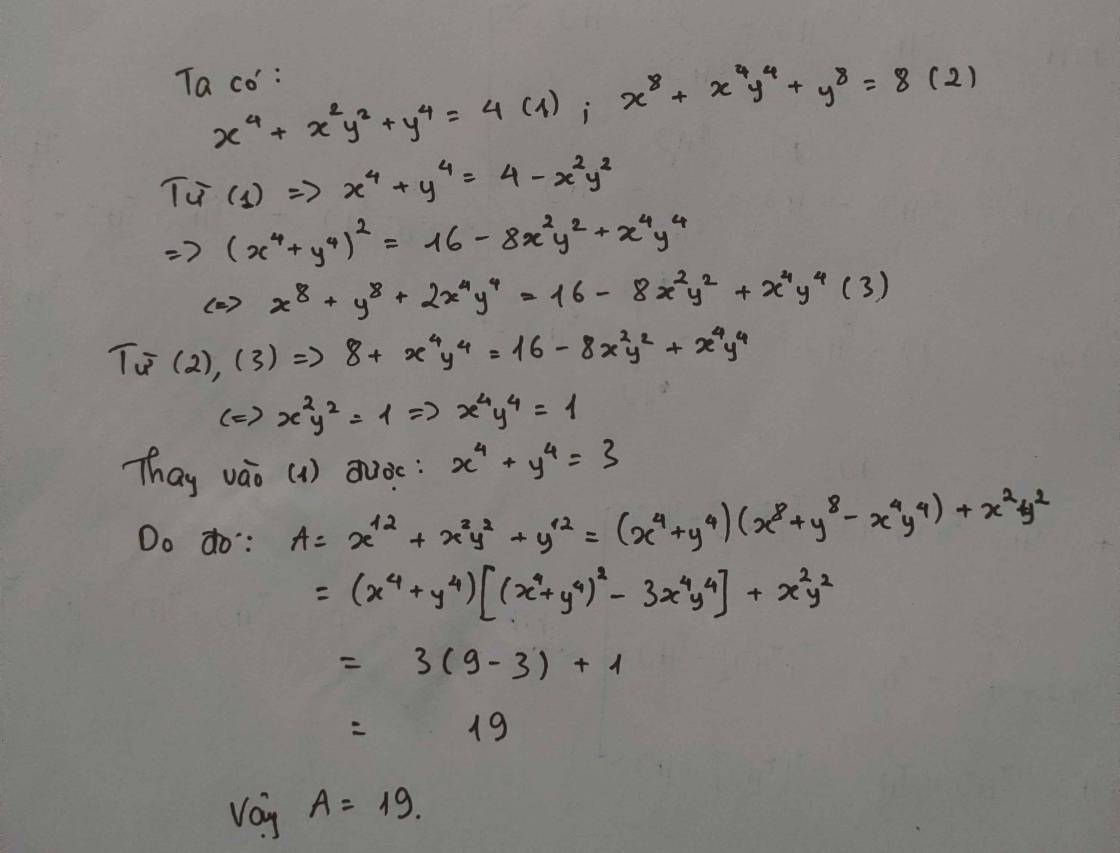
đề có vấn đề nha bạn
a, làm mẫu
\(x^4+x^2y^2+y^4=4\)
\(\Rightarrow x^4+2x^2y^2+y^4-\left(xy\right)^2=4\)
\(\Rightarrow\left(x^2+y^2\right)^2-\left(xy\right)^2=4\)
\(\Rightarrow\left(x^2+y^2+xy\right)\left(x^2+y^2-xy\right)=4\)
Từ đây dễ rồi tự làm