
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì góc ACB là có nội tiếp chắn nửa đường tròn của (O)
=> góc ACB= 90 độ
Xét (I) có góc MCN là góc nội tiếp chắn cung MN
mà góc MCN= 90 độ
=> MN là đường kính của (I)
=> 3 điểm M,I,N thẳng hàng
b) vì Δ CIN cân tại I( IC=IN=R)
=> góc ICN= góc INC
lại có Δ COB cân tại O(OC=OB=R)
=> góc OCB= góc OBC
=> góc INC= góc OBC ( cùng = góc OCB)
mà 2 góc này ở vị trí đồng vị của 2 đường thẳng MN và AB
=> MN // AB
lại có ID vuông góc với AB
=> ID vuông góc với MN( đpcm)

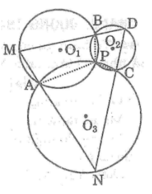
Gọi O1 , O2 ,O3 lần lượt là tâm của ba đường tròn
Ta có: ( O 1 ) cắt ( O 2 ) tại A, ( O 2 ) cắt ( O 3 ) tại C , ( O 3 ) cắt ( O 1 ) tại B
Suy ra: D là điểm nằm trên ( O 3 )
DB cắt ( O 1 ) tại M, DC cắt ( O 2 ) tại N
Nối MA, NA, PA, PB, PC ta có các tứ giác nội tiếp AMBP, BDCP và APCN
*Tứ giác APBM nội tiếp trong đường tròn ( O 1 ) nên ta có:



Vì tổng các góc trong tứ giác bằng \(360^0\) mà \(\widehat{CBE}+\widehat{EFC}=180^0\) nên suy ra \(\widehat{BCF}+\widehat{BEF}=180^0\)


gọi Ex là tia đối của tiếp tuyến EA
Ta có : \(\widehat{xED}=\frac{1}{2}sđ\widebat{ED}\); \(\widehat{EFD}=\frac{1}{2}sđ\widebat{ED}\)\(\Rightarrow\widehat{xED}=\widehat{EFD}\)( 1 )
Dễ thấy tứ giác AFOE nội tiếp
I là trung điểm của BC nên OI \(\perp\)BC \(\Rightarrow\)tứ giác AIOE nội tiếp
\(\Rightarrow\)5 điểm A,F,I,O,E cùng thuộc 1 đường tròn
\(\Rightarrow\)tứ giác AFIE nội tiếp \(\Rightarrow\)\(\widehat{EAI}=\widehat{EFI}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra : \(\widehat{xED}=\widehat{EAI}\Rightarrow ED//AC\)
Gọi N là giao điểm của AO và EF
Dễ chứng minh AN \(\perp\)EF
\(\DeltaẠNH~\Delta AIO\left(g.g\right)\Rightarrow\frac{AN}{AH}=\frac{AI}{AO}\Rightarrow AI.AH=AN.AO\)( 3 )
Ta có : \(AE^2=AN.AO\)( 4 )
Xét \(\Delta AEB\)và \(\Delta ACE\)có :
\(\widehat{EAC}\)( chung ) ; \(\widehat{AEB}=\widehat{ACE}=\frac{1}{2}sđ\widebat{EB}\)
\(\Rightarrow\Delta AEB~\Delta ACE\left(g.g\right)\)
\(\Rightarrow\frac{AE}{AB}=\frac{AC}{AE}\Rightarrow AE^2=AB.AC\)( 5 )
Từ ( 3 ) , ( 4 ) và ( 5 ) suy ra : AH.AI = AB.AC
đề bạn cho thiếu nhé. đoạn cuối AH. AI = AB . AC với H là giao điểm của AC và EF