
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình vẽ của bạn có thể được mô tả như sau:
- Góc BAx = 130 độ
- Góc ABy = 50 độ
- Góc Acz = 140 độ
- By song song với cz và Ax song song với Bx
- Ba vuông góc với AC

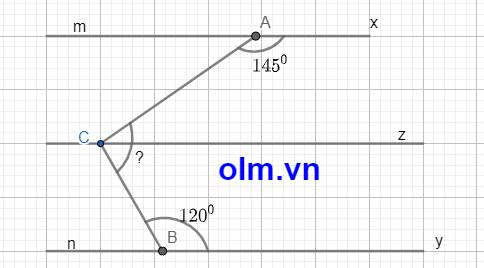
Ta có: \(\widehat{ACz}\) và \(\widehat{CAx}\) là hai góc trong cùng phía nên:
\(\widehat{ACz}\) + \(\widehat{CAx}\) = 1800 ⇒ \(\widehat{ACz}\) = 1800 - 1450 = 350
Mặt khác ta cũng có: \(\widehat{BCz}\) và \(\widehat{CBy}\) là hai góc trong cùng phía nên:
\(\widehat{BCz}\) + \(\widehat{CBy}\) = 1800 ⇒ \(\widehat{BCz}\) = 1800 - 1200 = 600
\(\widehat{ACB}\) = \(\widehat{ACz}\) + \(\widehat{BCz}\) = 350 + 600 = 950
Kết luận: \(\widehat{ACB}\) = 950


*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm

y x GT KL ACB=? xAC=120 độ yBC=140 độ Ax//Cz//By A C B z
\(\cdot\text{Do Ax//Cz}\)
\(\Rightarrow\widehat{xAC}+\widehat{ACz}=180^o\left(\text{trong cùng phía}\right)\left(1\right)\)
\(\text{Thay }\widehat{xAC}=120^o\text{ vào }\left(1\right)\)
\(\Rightarrow120^o+\widehat{ACz}=180^o\)
\(\Rightarrow\widehat{ACz}=180^o-120^o\)
\(\Rightarrow\widehat{ACz}=60^o\)
\(\cdot\text{Do By//Cz}\)
\(\Rightarrow\widehat{yCB}+\widehat{BCz}=180^o\left(\text{trong cùng phía}\right)\left(2\right)\)
\(\text{Thay }\widehat{yBC}=140^o\text{ vào }\left(2\right)\)
\(\Rightarrow140^o+\widehat{BCz}=180^o\)
\(\Rightarrow\widehat{BCz}=180^o-140^o\)
\(\Rightarrow\widehat{BCz}=40^o\)
\(\cdot\text{Lại có: }\widehat{ACz}+\widehat{BCz}=\widehat{ACB}\)
\(\text{Mà }\widehat{ACz}=60^o;\widehat{BCz}=40^o\)
\(\Rightarrow60^o+40^o=\widehat{ACB}\)
\(\Rightarrow\widehat{ACB}=100^o\)
\(\text{Vậy }\widehat{ACB}=100^o\)
\(\text{Tổng quát: Nếu }\widehat{A}+\widehat{B}+\widehat{C}=360^o\text{ thì ta luôn chứng minh được Ax//By/Cz}\)
\(\text{Và nếu Ax//By//Cz và biết 2 trong 3 góc thì ta luôn tìm ra được 1 góc còn lại. }\)