
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=b\cdot k;c=d\cdot k\)
\(\dfrac{a}{a+b}=\dfrac{bk}{bk+b}=\dfrac{bk}{b\left(k+1\right)}=\dfrac{k}{k+1}\)
\(\dfrac{c}{c+d}=\dfrac{dk}{dk+d}=\dfrac{dk}{d\left(k+1\right)}=\dfrac{k}{k+1}\)
Do đó: \(\dfrac{a}{a+b}=\dfrac{c}{c+d}\)
2: \(\dfrac{2a+b}{a-2b}=\dfrac{2\cdot bk+b}{bk-2b}=\dfrac{b\left(2k+1\right)}{b\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
\(\dfrac{2c+d}{c-2d}=\dfrac{2dk+d}{dk-2d}=\dfrac{d\left(2k+1\right)}{d\left(k-2\right)}=\dfrac{2k+1}{k-2}\)
Do đó: \(\dfrac{2a+b}{a-2b}=\dfrac{2c+d}{c-2d}\)
3: \(\dfrac{a+b}{a-b}=\dfrac{bk+b}{bk-b}=\dfrac{b\left(k+1\right)}{b\cdot\left(k-1\right)}=\dfrac{k+1}{k-1}\)
\(\dfrac{c+d}{c-d}=\dfrac{dk+d}{dk-d}=\dfrac{d\left(k+1\right)}{d\left(k-1\right)}=\dfrac{k+1}{k-1}\)
Do đó: \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
4: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5\cdot bk+3b}{5dk+3d}=\dfrac{b\left(5k+3\right)}{d\left(5k+3\right)}=\dfrac{b}{d}\)
\(\dfrac{5a-3b}{5c-3d}=\dfrac{5\cdot bk-3b}{5\cdot dk-3d}=\dfrac{b\left(5k-3\right)}{d\left(5k-3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)


Gọi \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=kb;c=kd\)(1)
Thay (1) vào ta có :
\(\frac{5a+3b}{5a-3b}=\frac{5kb+3b}{5kb-3b}=\frac{b\left(5k-3\right)}{b\left(5k-3\right)}=\frac{5k+3}{5k-3}\)(2)
\(\frac{5c+3d}{5c-3d}=\frac{5kd+3d}{5kd-3d}=\frac{d\left(5k+3\right)}{d\left(5k-3\right)}=\frac{5k+3}{5k-3}\)(3)
Từ (2) và (3)
\(\Rightarrow\frac{5a+3b}{5a-3b}=\frac{5c+3d}{5c-3d}\)
\(\RightarrowĐPCM\)

Bài 1:
a: =>7x-21=2x+2
=>5x=23
=>x=23/5
b: =>(x+5)^2=100
=>x+5=10 hoặc x+5=-10
=>x=-15 hoặc x=5

Ta có:
- \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
=>ad+ab<bc+ab
=>a(b+d)>b(a+c)
=>\(\frac{a}{b}< \frac{a+c}{b+d}\) (1)
- \(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
=>ad+cd<bc+cd
=>d(a+c)<c(b+d)
=>\(\frac{a+c}{b+d}< \frac{c}{d}\) (2)
Từ (1) và (2) => \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)(đpcm)
---------------
\(\frac{-1}{3}=\frac{-8}{24}>\frac{-9}{24}>\frac{-10}{24}>\frac{-11}{24}>\frac{-12}{24}=\frac{-1}{2}\)
---------------
\(\frac{-1}{5}< \frac{-1}{4}< \frac{-1}{3}< \frac{-1}{2}< -1< 0< \frac{1}{5}\)
\(\frac{-1}{2}=\frac{\left(-1\right).12}{2.12}=\frac{-12}{24}\)
\(\frac{-1}{3}=\frac{\left(-1\right).8}{3.8}=\frac{-8}{24}\)
\(\frac{-8}{24}< x< \frac{-12}{24}\)
\(\Rightarrow x=\left\{\frac{-9}{24};\frac{-10}{24};\frac{-11}{24}\right\}\)
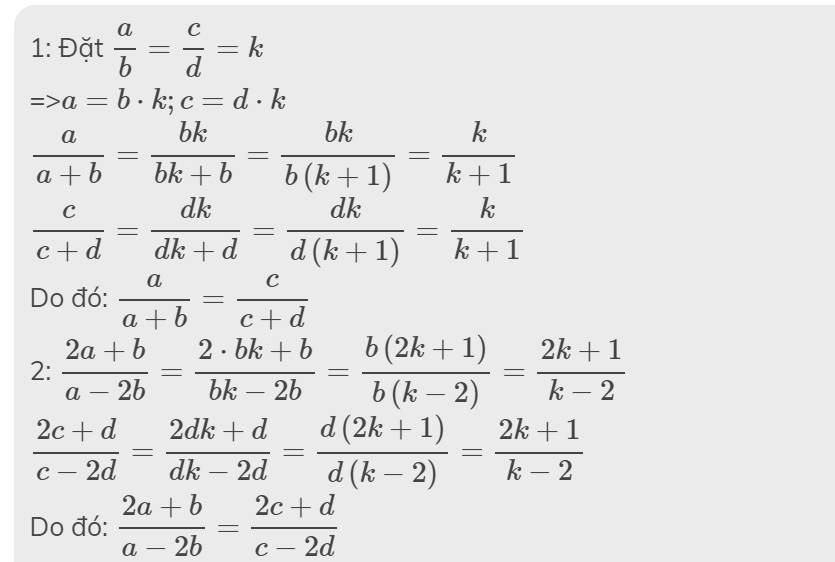
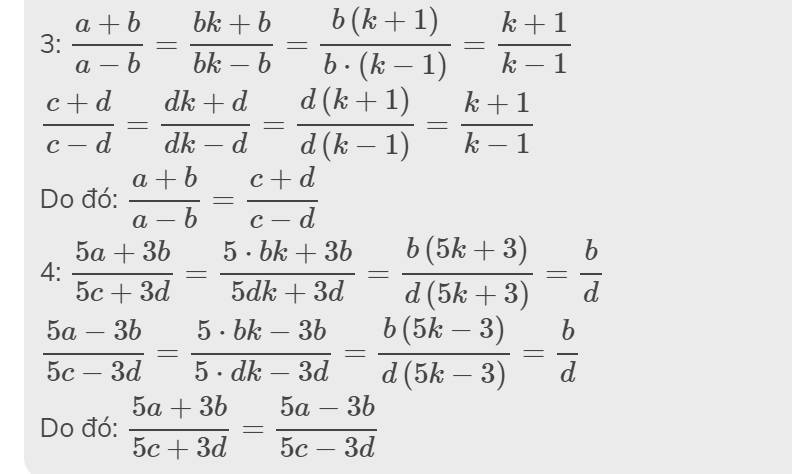
\(\frac{a}{b}=\frac{c}{d}=\frac{5a}{5b}=\frac{3c}{3d}=\frac{5a+3c}{5b+3d}=\frac{5a-3c}{5b-3d}\Rightarrow\frac{5a+3c}{5a-3c}=\frac{5b+3d}{5b-3d}\)