Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét △HBA và △ABC có
\(\widehat{AHB}=\widehat{BAC}=90^o\)
\(\widehat{B}\) là góc chung
⇒ ∆HBA ∾ ∆ABC (g-g)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: ΔABC vuông tại A
mà AH là đường cao
nên AH^2=HB*HC

c
AE = AH (gt)
AM = MH (gt)
\(\Rightarrow MH=\dfrac{1}{3}HE\)
Gọi N là trung điểm BH
Xét tam giác ABH có \(\left\{{}\begin{matrix}BN=NH\Rightarrow MN:đường.trung.bình.của.\Delta ABH\\AM=MH\Rightarrow MN//AB\end{matrix}\right.\)
=> \(MN\perp AC\)
Xét tam giác ANC có 2 đường cao là MN và AH
=> M là trực tâm
=> MC \(\perp\) AN
Có AN là đường trung bình tam giác BEH => AN//BE
=> AM // BE

cho mình hỏi đề bạn viết có đúng không vậy
Cho △ABC vuông tại A (AB<AC) có đường cao AH
a) Chứng minh : △HBA=△ABC ( chứng minh kiểu gì)
b)Chứng minh: AH2=HB.HC
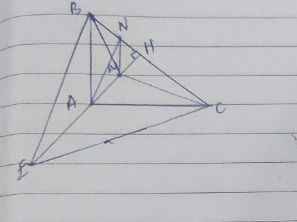
c)Gọi E là điểm đối xứng với H qua điểm A, M là trung điểm của AH. Chứng minh CM⊥BE tại K
có hình vẽ luôn càng tốt ạ
Ngủ rồi