
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp ấn:D
`(3x-1)^2=64`
`<=>` $\left[ \begin{array}{l}3x-1=8\\3x-1=-8\end{array} \right.$
`<=>` $\left[ \begin{array}{l}3x=9\\3x=-7\end{array} \right.$
`<=>` $\left[ \begin{array}{l}x=3\\x=-\dfrac73\end{array} \right.$


\(\left|a-1,74\right|\cdot\left|b^3+64\right|=0\)
\(\Leftrightarrow\begin{cases}a-1,74=0\\b^3+64=0\end{cases}\)\(\Leftrightarrow\begin{cases}a=1,74\\b=-4\end{cases}\)

Có: \(\left|a-1,74\right|\ge0;\left|b^3+64\right|\ge0\) với mọi a; b
Mà theo đề bài: |a - 1,74| + |b3 + 64| = 0
\(\Rightarrow\begin{cases}\left|a-1,74\right|=0\\\left|b^3+64\right|=0\end{cases}\)\(\Rightarrow\begin{cases}a-1,74=0\\b^3+64=0\end{cases}\)\(\Rightarrow\begin{cases}a=1,74\\b^3=-64\end{cases}\)\(\Rightarrow\begin{cases}a=1,74\\b=-8\end{cases}\)
Vậy a = 1,74; b = -8 thỏa mãn đề bài
Tớ đăng lên cho vui thôi, vì tớ chán quá. Vì cái này quá dễ rồi mà, việc gì phải hỏi nữa. Nhưng dù gì cg cảm ơn các bn đã tl câu hỏi của mk.
![]()

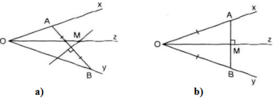
Tìm M khi OA = OB
Nếu OA = OB thì ∆AOB cân tại O nên tia phân giác góc xOy cũng là trung trực của AB.
Do đó mọi điểm trên tia phân giác góc xOy sẽ cách đều hai cạnh Ox, Oy và cách đều hai điểm A và B.
Vậy khi OA = OB thì có vô số điểm M thỏa mãn các điều kiện ở câu a.
Ta có: \(\left|a-1.47\right|\ge0\)
\(\left|b^3+64\right|\ge0\)
=> |a+1.47|+|b^3+64|=0
<=>\(\hept{\begin{cases}a-1.47=0\\b^3+64=0\end{cases}}\)
Giải 2 PT ta được:a=1.47
b=-4
Ok nha bạn :)
\(\left|a-1,47\right|+\left|b^3+64\right|=0\)
Do vế trái không âm nên
\(\Rightarrow\hept{\begin{cases}a-1,47=0\\b^3+64=0\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=1,47\\b=-4\end{cases}}\)