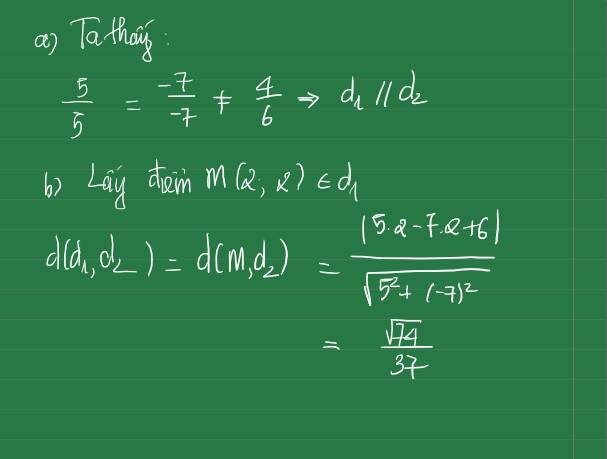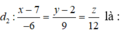Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(-3;1\right)\)
\(\overrightarrow{AC}=\left(x-1;-5\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{x-1}{-3}=\dfrac{-5}{1}\)
=>x-1=15
=>x=16

a) Nếu b = 0 và \(a \ne 0\) thì phương trình đường thẳng \(\Delta \) trở thành \(ax + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \(Oy\) và cắt trục \({\rm{O}}x\) tại điểm \(\left( { - \frac{c}{a};0} \right)\).
b) \(b \ne 0\) và a = 0 thì phương trình đường thẳng \(\Delta \) trở thành \(by + c = 0\) . Khi đó đường thẳng \(\Delta \) song song hoặc trùng với trục \({\rm{O}}x\) và cắt trục \(Oy\) tại điểm \(\left( {0; - \frac{c}{b}} \right)\).
c) Nếu \(b \ne 0\) và \(a \ne 0\)thì phương trình đường thẳng \(\Delta \) có thể viết thành \(y = - \frac{a}{b}x - \frac{c}{b}\). Khi đó, đường thẳng \(\Delta \) là đồ thị hàm số bậc nhất \(y = - \frac{a}{b}x - \frac{c}{b}\)vời hệ số góc là \(k = - \frac{a}{b}\).

Thay tọa độ A vào vế trái pt d ta được \(3.1+4.3-5=10>0\)
Để A; B nằm cùng phía với d
\(\Leftrightarrow3.2+4.m-5>0\)
\(\Leftrightarrow4m>-1\Rightarrow m>-\frac{1}{4}\)

a) Ta có: \(\overrightarrow {AB} = \left( {6;2} \right),\overrightarrow {AC} = \left( {4; - 6} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Do G là trọng tâm tam giác ABC nên \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{ - 2 + 4 + 2}}{3} = \frac{4}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{3 + 5 + \left( { - 3} \right)}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy \(G\left( {\frac{4}{3};\frac{5}{3}} \right)\)
c) Ta có: \(\overrightarrow {AB} = \left( {6;2} \right),\overrightarrow {AC} = \left( {4; - 6} \right),\overrightarrow {BC} = \left( { - 2; - 8} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{6^2} + {2^2}} = \sqrt {40} \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{4^2} + {{\left( { - 6} \right)}^2}} = \sqrt {52} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 8} \right)}^2}} = \sqrt {68} \end{array}\)
Ta có:
\(\begin{array}{l}\cos \widehat {BAC} = \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \frac{{6.4 + 2.\left( { - 6} \right)}}{{\sqrt {{6^2} + {2^2}} .\sqrt {{4^2} + {{\left( { - 6} \right)}^2}} }} \approx 0,263 \Rightarrow \widehat {BAC} \approx {74^o}\\\cos \widehat {ABC} = \cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\left( { - 6} \right).\left( { - 2} \right) + \left( { - 2} \right).\left( { - 8} \right)}}{{\sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 8} \right)}^2}} }} \approx 0,47 \Rightarrow \widehat {ABC} \approx {62^o}\end{array}\)
Áp dụng tính chất tổng ba góc trong một tam giác ta có: \(\widehat {ACB} \approx {180^o} - {74^o} - {62^o} \approx {44^o}\)

Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
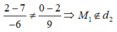
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.