M
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
13 tháng 11 2023
Ta có:
\(A=1+2+2^2+...+2^{2002}\)
\(2A=2+2^2+2^3+...+2^{2003}\)
\(2A-A=\left(2+2^2+2^3+...+2^{2003}\right)-\left(1+2+2^2+....+2^{2002}\right)\)
\(A=2^{2003}-1\)
Mà: \(2^{2003}=2^{2003}\)
\(\Rightarrow2^{2003}-1< 2^{2003}\)
\(\Rightarrow A< B\)
KV
26 tháng 12 2022
a) A = 2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰²²
2A = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰²³
A = 2A - A
= (2 + 2² + 2³ + 2⁴ + ... + 2²⁰²³) - (2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰²²)
= 2²⁰²³ - 2⁰
= 2²⁰²³ - 1
Vậy A = B
b) A = 2021 . 2023
= (2022 - 1).(2022 + 1)
= 2022.(2022 + 1) - 2022 - 1
= 2022² + 2022 - 2022 - 1
= 2022² - 1 < 2022²
Vậy A < B
HL
2
KV
14 tháng 11 2023
A = 2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰¹⁰
⇒ 2A = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰¹¹
⇒ A = 2A - A = (2 + 2² + 2³ + 2⁴ + ... + 2²⁰¹¹) - (2⁰ + 2¹ + 2² + 2³ + ... + 2²⁰¹⁰)
= 2²⁰¹¹ - 2⁰
= 2²⁰¹¹ - 1
= B
Vậy A = B
KV
9 tháng 1
Bài 1
a) S = 1 + 2 + 2² + 2³ + ... + 2²⁰²³
2S = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰²⁴
S = 2S - S = (2 + 2² + 2³ + ... + 2²⁰²⁴) - (1 + 2 + 2² + 2³)
= 2²⁰²⁴ - 1
b) B = 2²⁰²⁴
B - 1 = 2²⁰²⁴ - 1 = S
B = S + 1
Vậy B > S
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1
a,
\(S=1+2+2^2+...+2^{2023}\)
\(2S=2+2^2+2^3+...+2^{2024}\)
\(\Rightarrow S=2^{2024}-1\)
b.
Do \(2^{2024}-1< 2^{2024}\)
\(\Rightarrow S< B\)
2.
\(H=3+3^2+...+3^{2022}\)
\(\Rightarrow3H=3^2+3^3+...+3^{2023}\)
\(\Rightarrow3H-H=3^{2023}-3\)
\(\Rightarrow2H=3^{2023}-3\)
\(\Rightarrow H=\dfrac{3^{2023}-3}{2}\)
T
2 tháng 1
\(A=2+2^2+2^3+\dots+2^{60}\\2A=2^2+2^3+2^4+\dots+2^{61}\\2A-A=(2^2+2^3+2^3+\dots+2^{61})-(2+2^2+2^3+\dots+2^{60})\\A=2^{61}-2\)
Ta thấy: \(2^{61}-2< 2^{61}\)
\(\Rightarrow A< B\)
2 tháng 1
A=2+22+23+...+260
\(\Rightarrow\)2A=22+23+24+...+261
\(\Rightarrow\)2A-A=(22+23+24+...+261)-(2+22+2324+...+260)
\(\Rightarrow\)A=261-2
Mà 261-2<261 nên A<B
Vậy A<B
CM
4 tháng 2 2019
A=4+22+23+....+220
2A=8+23+24+...+221
=> A+2A-A = (8+23+24+...+221) - (4+22+23+....+220)
=>A=221+8 - (22+4)=221
=>A là 1 lũy thừa của 2
T
1
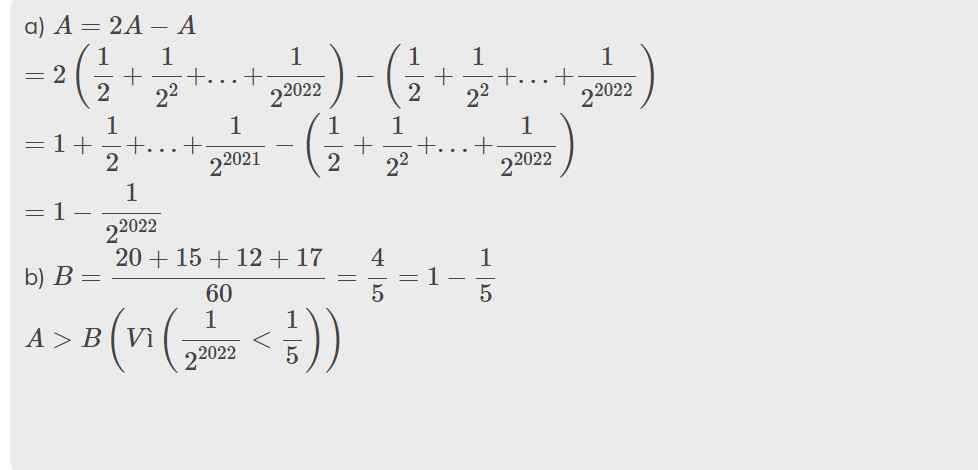
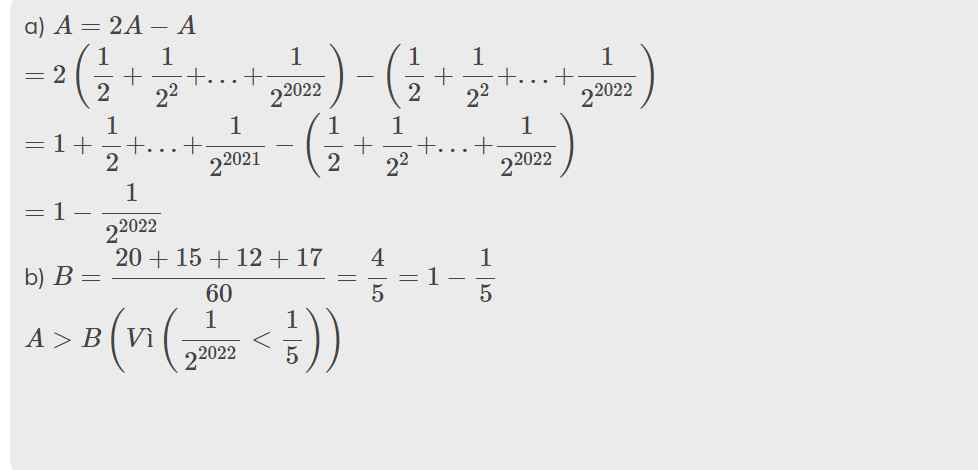
`2A=2 + 2^2 + 2^3 + ... + 2^2023`
`\rightarrow 2A - A = (2^2023 - 2^2022 + 2^2022 - 2^2021 + 2^2021 - ... -1)`
`A = 2^2023 - 1 = B`
`*2^2023` là `2^(2023)` nhé