Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

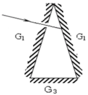
Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G3 theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy
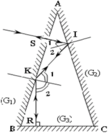
Tại I : I ^ 1 = I ^ 2 = A ^
Tại K: K ^ 1 = K ^ 2
Mặt khác K ^ 1 = I ^ 1 + I ^ 2 = 2 A ^
Do KR^BC ⇒ K ^ 2 = B ^ = C ^
Þ B ^ = C ^ = 2 A ^
Trong DABC có A ^ + B ^ + C ^ = 180 0
A ^ + 2 A ^ + 2 A ^ = 5 A ^ = 180 0 ⇒ A ^ = 180 0 5 = 36 0 ⇒ B ^ = C ^ = 2 A ^ = 72 0

S R G1 G2 N N' I I' i i' i2 i2'
a, Đầu tiên vẽ tia tới chiếu đến gương G1 tại I, rồi phản đến gương G2 tại điểm I' , rồi phản xạ tiếp qua điểm R
b, Ta có tia pháp tuyến \(NI\perp I\) (G1) , \(NI'\perp I'\left(G2\right)\)
mà 2 gương G1 , G2 vuông góc vói nhau
\(\Rightarrow\left\{{}\begin{matrix}i=90^o-45^o=45^o\\i=i'\Leftrightarrow i'=45^o\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}i2=90^o-45^o=45^o\\i2=i2'\Leftrightarrow i2'=45^o\end{matrix}\right.\)
Góc tạo bởi tia tới SI và tia phản xạ cuối cùng trên gương G2 : \(45^o+45^o+45^o+45^o=180^o\)
Tham khảo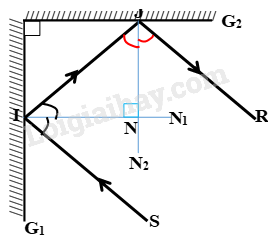
Do hai gương đặt vuông góc với nhau nên hai pháp tuyến IN1IN1 và JN2JN2 cũng vuông góc với nhau.
Định luật phản xạ tại gương G1G1:
ˆSIN=ˆNIJ⇒ˆSIJ=2ˆNIJ(1)SIN^=NIJ^⇒SIJ^=2NIJ^(1)
Định luật phản xạ tại gương G2G2:
ˆIJN=ˆNJR⇒ˆIJR=2ˆIJN(2)IJN^=NJR^⇒IJR^=2IJN^(2)
ΔIJNΔIJN vuông tại NN:
ˆNIJ+ˆNJI=900NIJ^+NJI^=900
⇒ˆSIJ+ˆIJR=2ˆNIJ+2ˆNJI=2(ˆNIJ+ˆNJI)=1800⇒SIJ^+IJR^=2NIJ^+2NJI^=2(NIJ^+NJI^)=1800
Vậy tia tới SISI song song với tia phản xạ JRJR. Góc tạo bởi tia tới SISI và tia phản xạ cuối cùng trên gương G2G2 có giá trị 1800

Vì sau khi phản xạ lần lượt trên các gương, tia phản xạ ló ra ngoài lỗ S trùng đúng với tia chiếu vào. Điều đó cho thấy trên từng mặt phản xạ có sự trùng nhau của tia tới và tia ló. Điều này chỉ xảy ra khi tia KR tới gương G3 theo hướng vuông góc với mặt gương. Trên hình vẽ ta thấy
Tại I : ˆI1=ˆI2=ˆAI^1=I^2=A^
Tại K: ˆK1=ˆK2K^1=K^2
Mặt khác ˆK1=ˆI1+ˆI2=2ˆAK^1=I^1+I^2=2A^
Do KR^BC ⇒ˆK2=ˆB=ˆC⇒K^2=B^=C^
Þ ˆB=ˆC=2ˆAB^=C^=2A^
Trong DABC có ˆA+ˆB+ˆC=1800A^+B^+C^=1800
ˆA+2ˆA+2ˆA=5ˆA=1800⇒ˆA=18005=360ˆ⇒B=ˆC=2ˆA=720A^+2A^+2A^=5A^=1800⇒A^=18005=360⇒B^=C^=2A^=720
ơ chỉ có chừng ấy thôi hả bạn còn tính các góc tạo bởi các mặt gương nữa thì sao bạn