Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

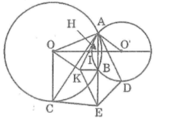
Gọi H là giao điểm của AB và OO’
Vì OO’ là đường trung trực của AB nên OO’ ⊥ AB tại H
Ta có: HA = HB
I là trung điểm của OO’ nên IH ⊥ AB (1)
Trong tam giác ABK, ta có:
HA = HB (chứng minh trên)
IA = IK (tính chất đối xứng tâm)
Suy ra IH là đường trung bình của tam giác ABK
Suy ra IH // BK (2)
Từ (1) và (2) suy ra: AB ⊥ KB

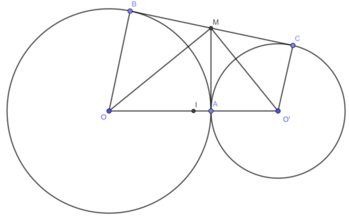
Ta có:
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM

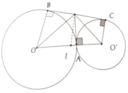
a, Chứng minh được tương tự câu 1a,
=> O ' M O ^ = 90 0
Áp dụng hệ thức lượng trong tam giác vuông tính được MA = R r
b, Chứng minh
S
B
C
O
O
'
=
R
+
r
R
r
c, Chứng minh được: ∆BAC:∆OMO’ => S B A C S O M O ' = B C O O ' 2
=> S B A C = S O M O ' . B C 2 O O ' 2 = 4 R r R r R + r
d, Tứ giác OBCO’ là hình thang vuông tại B và C có IM là đường trung bình => IM ⊥ BC = {M}

a, HS tự làm
b, HS tự làm
c, Chú ý hình thang vuông OEFO’ và xét đường trung bình của hình thang này
d, Từ I kẻ đường thảng song song với EF cắt OE tại M , cắt O’F tại N
Đặt BH=2R; CH= 2R’
∆IOM vuông tại M có:
I M 2 = I O 2 - O M 2 = R + r 2 - R - r 2 = 4 R r
Tương tự , ∆ION có I N 2 = 4 R ' r
Suy ra IM+IN=EF=AH
Vậy 2 R r + 2 R ' r = 2 R R '
=> r R + R ' = R R '
=> r = R R ' R + R ' 2