Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét (O) có
MA,MN là tiếp tuyến
=>MA=MN
mà OA=ON
nên OM là đường trung trực của AN
=>OM\(\perp\)AN(1)
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
=>AN\(\perp\)NB(2)
Từ (1) và (2) suy ra OM//NB
b: Xét ΔMAO vuông tại A và ΔKOB vuông tại O có
AO=OB
\(\widehat{AOM}=\widehat{OBK}\)
Do đó: ΔMAO=ΔKOB
=>MA=KO
Xét tứ giác MAOK có
MA//OK
MA=OK
Do đó: MAOK là hình bình hành
mà \(\widehat{MAO}=90^0\)
nên MAOK là hình chữ nhật
=>KM\(\perp\)xy
Ta có
\(AB=AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì khoảng cách từ điểm đó đến hai tiếp điểm bằng nhau)
\(\Rightarrow\Delta ABC\) cân tại A (1)
AO là phân giác của \(\widehat{BAC}\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường nối điểm đó với tâm của đường tròn là phân iacs của góc tạo bởi 2 tiếp tuyến) (2)
Từ (1) và (2) \(\Rightarrow AH\perp BC\) (Trong tg cân đường phân giác của góc ở đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AHE}=90^o\) (*)
Ta có
\(OM=ON\) (Bán kính (O)) \(\Rightarrow\Delta OMN\) cân tại O
Ta có \(IM=IN\) (Giả thiết) => ON là đường trung tuyến của tg OMN
\(\Rightarrow OE\perp AN\) (Trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường cao, đường trung trực...)
\(\Rightarrow\widehat{AIE}=90^o\) (**)
Từ (*) và (**) => I và H cùng nhìn AE dưới hai góc bằng nhau và bằng 90 độ => I và H nằm trên đường tròn đường kính AE nên 4 điểm A;H;I;E cùng nằm trên 1 đường tròn
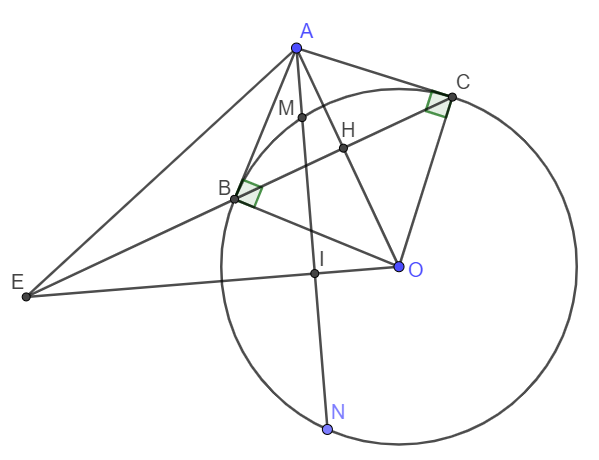
Cho đường tròn tâm bán kính và một điểm nằm ngoài đường tròn. Kẻ một đường thẳng đi qua và không đi qua , cắt đường tròn tại hai điểm phân biệt , ( nằm giữa và ). Từ vẽ hai tiếp tuyến và với (, là hai tiếp điểm). Đường thẳng cắt tại . Gọi là trung điểm của . Đường thẳng cắt đường thẳng tại . Chứng minh là tứ giác nội tiếp.
theo gt, ta co:
là trung điểm của
Ta có:
Mà OB ⊥ BC ⇒ IM ⊥ BC
Ta có:
IM ⊥ BC
BC ⋂ (I; IM) = {M}
Suy ra, BC là tiếp tuyến của đường tròn tâm I, bán kính IM
câu hổi là gì nhóc kém thế
hoc lop may