Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\overrightarrow{E_1}+\overrightarrow{E_2}=0\Rightarrow\overrightarrow{E_1}=-\overrightarrow{E_2}\)
Để \(\overrightarrow{E_1}\) ngược chiều \(\overrightarrow{E_2}\) thì điểm M nằm trên đường nối AB và nằm ngoài AB.
Có: \(E_1=E_2\) \(\Leftrightarrow k\dfrac{\left|q_1\right|}{r_1^2}=k\dfrac{\left|q_2\right|}{r_2^2}\) \(\Leftrightarrow\dfrac{4.10^{-8}}{r_1^2}=\dfrac{10^{-8}}{r_2^2}\) \(\Leftrightarrow r_1=2r_2\left(1\right)\)
Vì: \(\left|q_1\right|>\left|q_2\right|\) nên điểm M nằm ngoài AB và gần B hơn.
⇒ r1 - r2 = 6 (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}r_1=12\left(cm\right)\\r_2=6\left(cm\right)\end{matrix}\right.\)
Vậy: Vị trí cường độ điện trường bằng 0 cách q1 12cm, cách q2 6cm.

Điểm có cường độ điện trường bằng không, tức là:
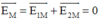
Suy ra: 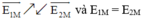
Do đó điểm này nằm trên đường thẳng nối hai điện tích .
Vì q1 và q2 trái dấu nên điểm này nằm ngoài đoạn thẳng nối hai điện tích và ở về phía gần q1 (vì q1 < | q2 |)
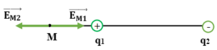
Ta có:
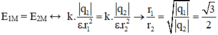
Và r2 – r1 = 10cm (2)
Từ (1) và (2) ta tìm được r1 ≈ 64,6 cm và r2 = 74,6 cm.
Tại điểm đó không có điện trường vì EM = 0.
Đáp số: r1 ≈ 64,64 cm ; r2 ≈ 74,64 cm.

Đáp án: A
Để cường độ điện trường tại M bằng 0 thì hai vecto E 1 do q1 gây ra và E 2 do q2 gây ra phải ngược chiều và cùng độ lớn nên M nằm trên đường thẳng AB và ngoài đoạn AB
Do |q2| > |q1| nên r1 < r2 => r1 = r2 - AB,
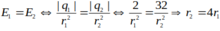
=>![]() và r1 = 10 cm
và r1 = 10 cm

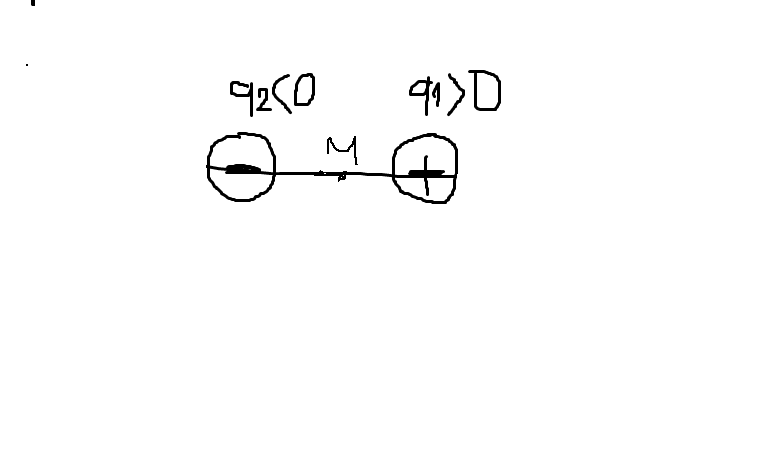
Để lực tổng hợp tác dụng lên điện tích bằng q0=0 thì \(\overrightarrow{F_{10}}+\overrightarrow{F_{20}}=\overrightarrow{0}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{F_{10}}\uparrow\downarrow\overrightarrow{F_{20}}\\F_{10}=F_{20}\end{matrix}\right.\)
Ta có \(MB-MA=r_1-r_2=10\) (1)
Mà \(F_{10}=F_{20}\Rightarrow k\cdot\dfrac{\left|q_1q_0\right|}{r^2_1}=k\cdot\dfrac{\left|q_2q_0\right|}{r^2_2}\)\(\Rightarrow\dfrac{r_1}{r_2}=2\) (2)
Từ 1 và 2 \(\Rightarrow\left\{{}\begin{matrix}r_1=20cm\\r_2=10cm\end{matrix}\right.\)
\(\Rightarrow\) M cách A 10cm và cách B 20cm

a) Véc tơ lực tác dụng của điện tích q 1 l ê n q 2 có phương chiều như hình vẽ:

Có độ lớn: F 12 = k . | q 1 . q 2 | A B 2 = 9.10 9 .16.10 − 6 .4.10 − 6 0 , 3 2 = 6 , 4 ( N ) .
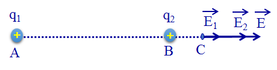
b) Các điện tích q 1 v à q 2 gây ra tại C các véc tơ cường độ điện trường E 1 → và E 2 → có phương chiều như hình vẽ:
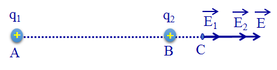
Có độ lớn: E 1 = k | q 1 | A C 2 = 9.10 9 .16.10 − 6 0 , 4 2 = 9 . 10 5 ( V / m ) ;
E 2 = k | q 2 | B C 2 = 9.10 9 .4.10 − 6 0 , 1 2 = 36 . 10 5 ( V / m ) ;
Cường độ điện trường tổng hợp tại C là:
E → = E 1 → + E 2 → có phương chiều như hình vẽ, có độ lớn:
E = E 1 + E 2 = 9 . 10 5 + 36 . 10 5 - 45 . 10 5 ( V / m ) .
c) Gọi E 1 → và E 2 → là cường độ điện trường do q 1 v à q 2 gây ra tại M thì cường độ điện trường tổng hợp do q 1 v à q 2 gây ra tại M là: E → = E 1 → + E 2 → = 0 → ð E 1 → = - E 2 → ð E 1 → và E 2 → phải cùng phương, ngược chiều và bằng nhau về độ lớn. Để thỏa mãn các điều kiện đó thì M phải nằm trên đường thẳng nối A, B; nằm trong đoạn thẳng AB (như hình vẽ).
Với E 1 ' = E 2 ' ⇒ 9 . 10 9 . | q 1 | A M 2 = 9 . 10 9 . | q 2 | ( A B − A M ) 2
⇒ A M A B − A M = | q 1 | | q 2 | = 2 ⇒ A M = 2. A B 3 = 2.30 3 = 20 ( c m ) .
Vậy M nằm cách A 20 cm và cách B 10 cm.