Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương trình đường thẳng AB: qua A( 2;2) ; VTCP ( 3; -1) nên có VTPT ( 1;3)
Phương trình: 3( x-2) -1( y-2) = 0 hay 3x- y -4= 0.
Điểm C (2t-8; t) thuộc d và ![]()
Diện tích tam giác ABC:
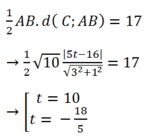
Mà điểm C có hoành độ dương nên chọn t= 10 ; khi đó C( 12; 10) .

ĐÁP ÁN B.
Do C nằm trên đường thẳng ∆: x – 2y + 3 = 0 nên ta gọi tọa độ C là C(2y – 3; y).
Mà A B = ( − 2 + 4 ) 2 + ( 1 + 1 ) 2 = 2 2
Phương trình AB: qua A( - 4; -1) và nhận VTCP A B → ( 2 ; 2 ) nên có VTPT là: n → ( 1 ; − 1 ) :
1( x+ 4) – 1 ( y + 1) = 0 hay x – y + 3 = 0
d ( C ; A B ) = 2 y − 3 − y + 3 2 = y 2
Theo đầu bài ta có:
40 = S = 1 2 . A B . d ( C ; A B ) = 1 2 . 2 2 . y 2 ⇔ y = 40 ⇔ y = ± 40

Ta có B(a;2-a) ; C(b;8-b)
Để tam giác ABC vuông cân tại A
\(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{AB}=\overrightarrow{0}\\\overrightarrow{AC}=\overrightarrow{AB}\end{matrix}\right.\) bạn thay vào giải hpt bằng p2 thế nhé

Mik đang bận nên chỉ có HD thôi ạ :
-Viết p/t đ/t d ; biểu diễn tọa độ P theo d
- Tính MN ; NP ; MP
- ADCT : \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) ( p = a + b + c / 2 )
GPT tìm tọa độ P
\(\overrightarrow{NM}=\left(3;3\right)\Rightarrow MN=\sqrt{3^2+3^2}=3\sqrt{2}\) và đường thẳng MN nhận (1;-1) là 1 vtpt
Phương trình MN:
\(1\left(x-2\right)-1\left(y-2\right)=0\Leftrightarrow x-y=0\)
Do P thuộc (d) nên tọa độ có dạng: \(\left(-8+2t;t\right)\)
\(\Rightarrow d\left(P;MN\right)=\dfrac{\left|-8+2t-t\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\left|t-8\right|}{\sqrt{2}}\)
\(S_{MNP}=\dfrac{1}{2}.d\left(P;MN\right).MN=18\)
\(\Leftrightarrow\dfrac{1}{2}.\dfrac{\left|t-8\right|}{\sqrt{2}}.3\sqrt{2}=18\)
\(\Rightarrow\left|t-8\right|=12\Rightarrow\left[{}\begin{matrix}t=20\\t=-4\end{matrix}\right.\) (loại \(t=20\) do P có tung độ âm)
\(\Rightarrow P\left(-16;-4\right)\Rightarrow2a-13b=20\)

a) đặc C (x;y) , ta có : C \(\in\) (d) \(\Leftrightarrow x=-2y-1\)
vậy C (-2y -1 ; y ).
tam giác ABC cân tại C khi và chỉ khi
CA = CB \(\Leftrightarrow\) CA2 = CB2
\(\Leftrightarrow\) (3+ 2y + 1)2 + (- 1- y)2 = (- 1+ 2y + 1)2 + (- 2- y)2
\(\Leftrightarrow\) (4 + 2y)2 + (1 + y)2 = 4y2 + (2 + y)2
giải ra ta được y = \(\dfrac{-13}{14}\) ; x = \(-2\left(\dfrac{-13}{14}\right)-1=\dfrac{13}{7}-1=\dfrac{6}{7}\)
vậy C có tọa độ là \(\left(\dfrac{6}{7};\dfrac{-13}{14}\right)\)
b) xét điểm M (- 2t - 1 ; t) trên (d) , ta có :
\(\widehat{AMB}\) = 900 \(\Leftrightarrow\) AM2 + BM2 = AB2
\(\Leftrightarrow\) (4 + 2t)2 + (1 + t)2 + 4t2 + (2 + t)2 = 17
\(\Leftrightarrow\) 10t2 +22t + 4 = 0 \(\Leftrightarrow\) 5t2 + 11t + 2 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}t=\dfrac{-1}{5}\\t=-2\end{matrix}\right.\)
vậy có 2 điểm thỏa mãn đề bài là M1\(\left(\dfrac{-3}{5};\dfrac{-1}{5}\right)\) và M2\(\left(3;-2\right)\)

Câu 1 đề thiếu, điểm C thỏa mãn điều gì nữa? (ví dụ G là trọng tâm tam giác?)
Câu 2:
Do B, C đều thuộc d nên tọa độ có dạng: \(B\left(2b-3;b\right);C\left(2c-3;c\right)\) với \(b\ne c\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\left(2c-2;c-2\right)\\\overrightarrow{BC}=\left(2c-2b;c-b\right)\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{AC}.\overrightarrow{BC}=0\\AC=3BC\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left(2c-2\right)\left(2c-2b\right)+\left(c-2\right)\left(c-b\right)=0\\\left(2c-2\right)^2+\left(c-2\right)^2=9\left(2c-2b\right)^2+9\left(c-b\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4c-4+c-2=0\\\left(2c-2\right)^2+\left(c-2\right)^2=45\left(c-b\right)^2\end{matrix}\right.\)
\(\Rightarrow...\)

Phương trình đường thẳng BC: a(x-2) + b(y-2)=0
cos(BA;BC)=cos\(45^0\)=\(\dfrac{1}{\sqrt{2}}=\dfrac{\left|a-b\right|}{\sqrt{2\left(a^2+b^2\right)}}\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\\b=0\end{matrix}\right.\). Vì a,b không đồng thời bằng 0 nên suy ra \(\left[{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Vì tọa độ C có hoành độ x lớn hơn 2 nên phương trình đường thẳng BC là y=2.
Ta có:\(S_{ABC}=\dfrac{1}{2}AB.BC.sin45^0\)\(\Leftrightarrow2=\dfrac{1}{2}\sqrt{8}\sqrt{\left(x_C-2\right)^2}.\dfrac{\sqrt{2}}{2}\Leftrightarrow x_C=4\)
Vậy tọa độ C(4;2)

\(d1:x+y-2=0\Leftrightarrow y=-x+2\Rightarrow B\left(a;-b+2\right)\)
\(d2:x+y-8=0\Leftrightarrow y=-x+8\Rightarrow C\left(b;-b+8\right)\)
\(\Rightarrow AB=\sqrt{\left(a-2\right)^2+\left(-a+2-2\right)^2}\)
\(\Rightarrow AC=\sqrt{\left(b-2\right)^2+\left(-b+8-2\right)^2}\)
\(\Delta ABC\) \(vuông\) \(cân\) \(tạiA\Rightarrow\left\{{}\begin{matrix}AB^2=AC^2\\\overrightarrow{AB}.\overrightarrow{AC}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-2\right)^2+\left(-a\right)^2=\left(b-2\right)^2+\left(-b+8-2\right)^2\\\left(a-2\right)\left(b-2\right)+\left(-a\right)\left(-b+6\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=-1\\b=3\end{matrix}\right.\\\left\{{}\begin{matrix}a=3\\b=5\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}B\left(-1;3\right)\\C\left(3;5\right)\end{matrix}\right.\\\left\{{}\begin{matrix}B\left(3;-1\right)\\C\left(5;3\right)\end{matrix}\right.\end{matrix}\right.\)
Gọi \(C\left(x_c;y_c\right)\) \(\Rightarrow x_c-2y_c+8=0\) (1)
ta có độ dài đoạn \(AB\) bằng \(\sqrt{\left(5-2\right)^2+\left(1-2\right)^2}=\sqrt{10}\)
ta có : \(\overrightarrow{AB}\left(3;-1\right)\) \(\Rightarrow\overrightarrow{U}_{AB}\left(1;3\right)\)
\(\Rightarrow\) phương trình tổng quát của đường thẳng \(AB\) là :
\(\left(x-2\right)+3\left(y-2\right)=0\Leftrightarrow x+3y-8=0\)
\(\Rightarrow\) đường cao kẻ từ \(C\) có độ dài là : \(\dfrac{\left|x_c+3y_c-8\right|}{\sqrt{1^2+3^2}}.\sqrt{10}=7\)
\(\Leftrightarrow\left|x_c+3y_c-8\right|=7\) \(\Leftrightarrow\left[{}\begin{matrix}x_c+3y_c-8=7\left(2\right)\\x_c+3y_c-8=-7\left(3\right)\end{matrix}\right.\)
từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}x_c+3y_c=15\\x_c-2y_c=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_c=\dfrac{6}{5}\\y_c=\dfrac{23}{5}\end{matrix}\right.\)
từ (1) và (3) ta có hệ : \(\left\{{}\begin{matrix}x_c+3y_c=1\\x_c-2y_c=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_c=\dfrac{-22}{5}\\y_c=\dfrac{9}{5}\end{matrix}\right.\)
vậy có 2 điểm \(C\) thỏa mãn điều kiện bài toán là : \(C\left(\dfrac{6}{5};\dfrac{23}{5}\right);c\left(\dfrac{-22}{5};\dfrac{9}{5}\right)\)
Gọi \(C\left(x_c;y_c\right)\) \(\Rightarrow x-2y+8=0\) (1)
ta có độ dài của đoạn thẳng \(AB=\sqrt{\left(5-2\right)^2+\left(1-2\right)^2}=\sqrt{10}\)
ta có : \(\overrightarrow{AB}\left(3;-1\right)\) \(\Rightarrow VTPT\) của \(AB\) là \(\overrightarrow{U}_{AB}\left(1;3\right)\)
\(\Rightarrow\) phương trình tổng quát của đường thẳng \(AB\) là
\(\left(x-2\right)+3\left(y-2\right)=0\Leftrightarrow x+3y-8=0\)
\(\Rightarrow\) đường cao kẻ từ \(C\) có độ dài : \(\dfrac{\left|x_c+3y_c-8\right|}{\sqrt{1^2+3^2}}=\dfrac{17.2}{\sqrt{10}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_c+3y_c-8=34\left(2\right)\\x_c+3y_c-8=-34\left(3\right)\end{matrix}\right.\)
từ (1) và (2) ta có hệ : \(\left\{{}\begin{matrix}x_c-2y_c=-8\\x_c+3y_c=42\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_c=12\\y_c=10\end{matrix}\right.\)
từ (1) và (3) ta có hệ : \(\left\{{}\begin{matrix}x_c-2y_c=-8\\x_c+3y_c=-26\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_c=\dfrac{-76}{5}\\y_c=\dfrac{-18}{5}\end{matrix}\right.\)
vậy có 2 điểm \(C\) thỏa mãn điều kiện bài toán là : \(C\left(12;10\right);C\left(\dfrac{-76}{5};\dfrac{-18}{5}\right)\)
bài lm kia mk bị nhầm chút ; mk làm lại nha :((