K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 8 2023
5:
a: \(-120x^5y^4=20x^5y^2\cdot\left(-6y^2\right)\)
b: \(60x^6y^2=20x^5y^2\cdot3x\)
c: \(-5x^{15}y^3=20x^5y^2\cdot\left(-\dfrac{1}{4}x^{10}y\right)\)
d: \(2x^{12}y^{10}=20x^5y^2\cdot\left(\dfrac{1}{10}x^7y^8\right)\)
HT
2
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
\(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
\(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(b+1\right)}=\dfrac{b}{a}\)
T
12 tháng 1
d) Để phân thức \(\dfrac{4x^3+4x^2}{x^2-1}\) có nghĩa thì: \(x^2-1\ne0\Leftrightarrow x\ne\pm1\)
Khi đó: \(\dfrac{4x^3+4x^2}{x^2-1}=\dfrac{4x^2\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x^2}{x-1}\)
e) Để phân thức \(\dfrac{b^2+b}{a+ab}\) có nghĩa thì: \(a+ab\ne0\Leftrightarrow a\ne-ab\)
Khi đó: \(\dfrac{b^2+b}{a+ab}=\dfrac{b\left(b+1\right)}{a\left(1+b\right)}=\dfrac{b}{a}\)
T
3 tháng 12 2023
a) \(\left(x^2+x+1\right)\left(x^2+x+2\right)-12\)
Đặt: \(x^2+x+1=y\), khi đó biểu thức trở thành:
\(y\left(y+1\right)-12\)
\(=y^2+y-12\)
\(=y^2-3y+4y-12\)
\(=y\left(y-3\right)+4\left(y-3\right)\)
\(=\left(y-3\right)\left(y+4\right)\)
\(=\left(x^2+x+1-3\right)\left(x^2+x+1+4\right)\)
\(=\left(x^2+x-2\right)\left(x^2+x+5\right)\)
\(=\left(x^2-x+2x-2\right)\left(x^2+x+5\right)\)
\(=\left[x\left(x-1\right)+2\left(x-1\right)\right]\left(x^2+x+5\right)\)
\(=\left(x-1\right)\left(x+2\right)\left(x^2+x+5\right)\)
b) \(\left(x^2+2x\right)^2+9x^2+18x+20\)
\(=\left(x^2+2x\right)^2+9\left(x^2+2x\right)+20\)
Đặt: \(x^2+2x=a\), khi đó biểu thức trở thành:
\(a^2+9a+20\)
\(=a^2+4a+5a+20\)
\(=a\left(a+4\right)+5\left(a+4\right)\)
\(=\left(a+4\right)\left(a+5\right)\)
\(=\left(x^2+2x+4\right)\left(x^2+2x+5\right)\)
c) \(\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left[\left(x+2\right)\left(x+8\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
Đặt: \(x^2+10x+20=y\), khi đó biểu thức trở thành:
\(\left(y-4\right)\left(y+4\right)+16\)
\(=y^2-16+16\)
\(=y^2\)
\(=\left(x^2+10x+20\right)^2\)
$\text{#}Toru$
3 tháng 12 2023
\(x^3-y^3-z^3=3xyz\)
=>\(\left(x-y\right)^3-z^3+3xy\left(x-y\right)-3xyz=0\)
=>\(\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]+3xy\left(x-y-z\right)=0\)
=>\(\left(x-y-z\right)\left[x^2-2xy+y^2+xz-zy+z^2+3xy\right]=0\)
=>\(\left(x-y-z\right)\left(x^2+y^2+z^2+xy+xz-yz\right)=0\)
=>\(\left(x-y-z\right)\left(2x^2+2y^2+2z^2+2xy+2xz-2yz\right)=0\)
=>\(\left(x-y-z\right)\left[\left(x^2+2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(x^2+2xz+z^2\right)\right]=0\)
=>\(\left(x-y-z\right)\left[\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2\right]=0\)
=>\(\left[{}\begin{matrix}x-y-z=0\\\left(x+y\right)^2+\left(y-z\right)^2+\left(x+z\right)^2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=y+z\\y=z=-x\end{matrix}\right.\)
\(H=\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1-\dfrac{z}{x}\right)\)
\(=\dfrac{y-x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x-z}{x}\)
TH1: x=y+z
=>\(H=\dfrac{y-x}{y}\cdot\dfrac{x}{z}\cdot\dfrac{x-z}{x}\)
\(=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{y-x}{y}=\dfrac{y}{x}\cdot\dfrac{z}{x}\cdot\dfrac{-z}{y}=-1\)
TH2: y=z=-x
=>y+x+z=0(vô lý vì x,y,z đều dương)
Vậy: H=-1
8 tháng 12 2023
a: Xét ΔKAB và ΔKCD có
\(\widehat{KAB}=\widehat{KCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AKB}=\widehat{CKD}\)(hai góc đối đỉnh)
Do đó: ΔKAB đồng dạng với ΔKCD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: Ta có: \(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(\dfrac{KC}{KA}=\dfrac{KD}{KB}\)
=>\(\dfrac{KC}{KA}+1=\dfrac{KD}{KB}+1\)
=>\(\dfrac{KC+KA}{KA}=\dfrac{KD+KB}{KB}\)
=>\(\dfrac{AC}{KA}=\dfrac{BD}{KB}\)
=>\(\dfrac{AK}{AC}=\dfrac{BK}{BD}\left(1\right)\)
Xét ΔADC có IK//DC
nên \(\dfrac{AK}{AC}=\dfrac{IK}{DC}\left(2\right)\)
Xét ΔBDC có KQ//DC
nên \(\dfrac{KQ}{DC}=\dfrac{BK}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra IK=KQ
23 tháng 9 2021
40: Ta có: \(A=27x^3+8y^3-3x-2y\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2\right)-\left(3x+2y\right)\)
\(=\left(3x+2y\right)\left(9x^2-6xy+4y^2-1\right)\)
HT
1
4 tháng 1
a: Xét ΔMQP có
H,I lần lượt là trung điểm của MQ,MP
=>HI là đường trung bình của ΔMQP
=>HI//QP và HI=QP/2
Xét ΔPMN có
I,K lần lượt là trung điểm của PM,PN
=>IK là đường trung bình của ΔPMN
=>IK//MN và \(IK=\dfrac{MN}{2}\)
b: H,I,K thẳng hàng
mà HI//PQ và IK//MN
nên HI//MN
Ta có: HI//MN
HI//PQ
Do đó: MN//PQ
HH
0
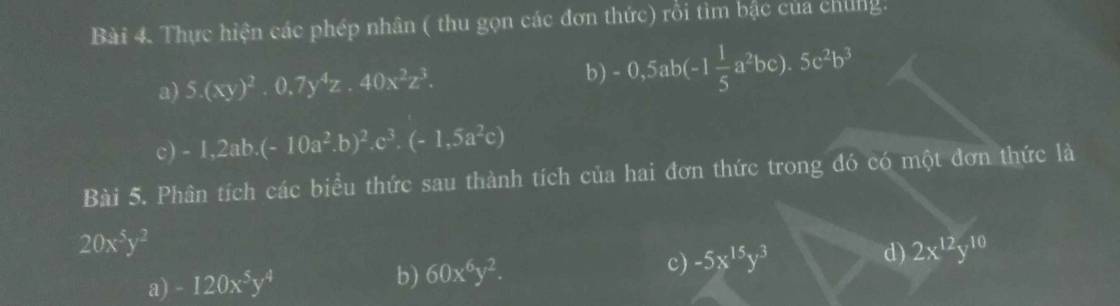
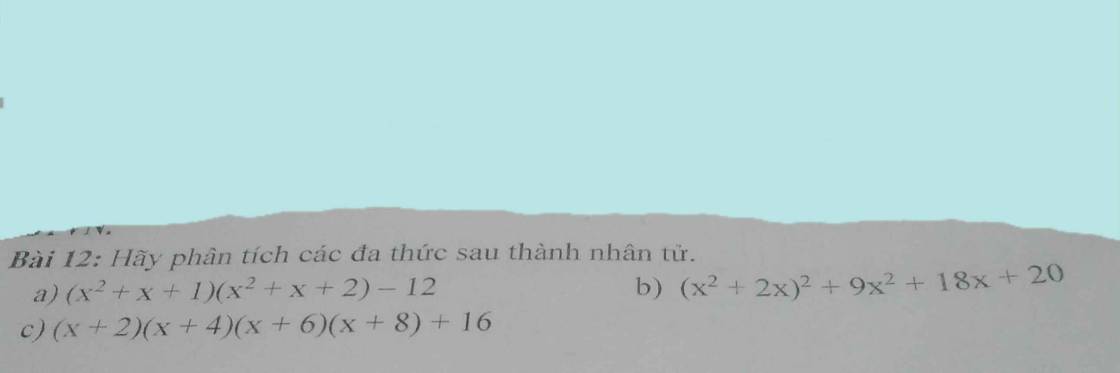
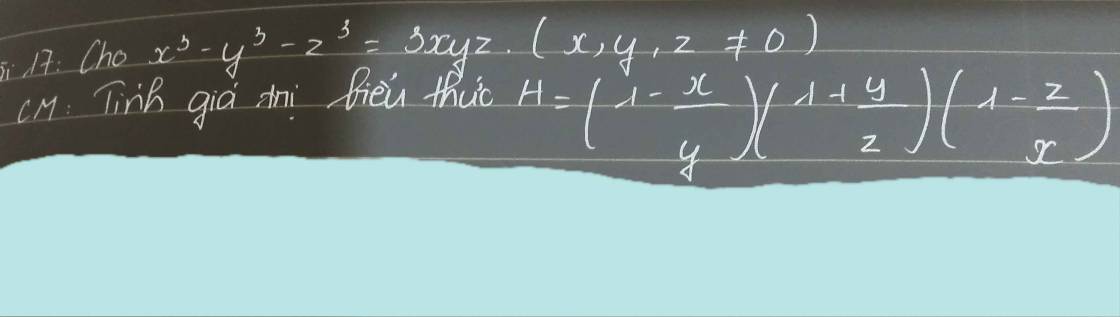
Bài 13:
a) \(x^3-49x=0\)
\(\Leftrightarrow x\left(x^2-49\right)=0\)
\(\Leftrightarrow x\left(x+7\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+7=0\\x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-7\\x=7\end{matrix}\right.\)
b) \(x^3-3x^2+3x-1=0\)
\(\Leftrightarrow x^3-3\cdot x^2\cdot1+3\cdot x\cdot1^2-1^3=0\)
\(\Leftrightarrow\left(x-1\right)^3=0\)
\(\Leftrightarrow x-1=0\)
\(\Leftrightarrow x=1\)
c) \(x^3+6x^2+9x=0\)
\(\Leftrightarrow x\left(x^2+6x+9\right)=0\)
\(\Leftrightarrow x\left(x^2+2\cdot3\cdot x+3^2\right)=0\)
\(\Leftrightarrow x\left(x+3\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
d) \(\left(x+5\right)^2-16x^2=0\)
\(\Leftrightarrow\left(x+5\right)^2-\left(4x\right)^2=0\)
\(\Leftrightarrow\left(x+5-4x\right)\left(x+5+4x\right)=0\)
\(\Leftrightarrow\left(5-3x\right)\left(5x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5-3x=0\\5x+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=5\\5x=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)
12:
a: \(4x^2+4x+1=0\)
=>\(\left(2x\right)^2+2\cdot2x\cdot1+1^2=0\)
=>\(\left(2x+1\right)^2=0\)
=>2x+1=0
=>2x=-1
=>\(x=-\dfrac{1}{2}\)
b: \(x^2-2x=-1\)
=>\(x^2-2x+1=0\)
=>\(x^2-2\cdot x\cdot1+1^2=0\)
=>\(\left(x-1\right)^2=0\)
=>x-1=0
=>x=1
c: \(-x^2+10x=25\)
=>\(-x^2+10x-25=0\)
=>\(x^2-10x+25=0\)
=>\(x^2-2\cdot x\cdot5+5^2=0\)
=>\(\left(x-5\right)^2=0\)
=>x-5=0
=>x=5
d: \(12x-4x^2=9\)
=>\(-4x^2+12x-9=0\)
=>\(4x^2-12x+9=0\)
=>\(\left(2x\right)^2-2\cdot2x\cdot3+3^2=0\)
=>\(\left(2x-3\right)^2=0\)
=>2x-3=0
=>2x=3
=>x=3/2