
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. \(C=\dfrac{n+1}{n-2}\) \(\left(n\ne2\right)\)
\(C=\dfrac{n-2+3}{n-2}=\dfrac{n-2}{n-2}+\dfrac{3}{n-2}=1+\dfrac{3}{n-2}\)
Để C nguyên thì \(\dfrac{3}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
`@n-2=1->n=3(n)`
`@n-2=-1->n=1(n)`
`@n-2=3->n=5(n)`
`@n-2=-3->n=-1(n)`
Vậy \(n\in\left\{3;1;5;-1\right\}\) thì C nguyên
b.\(D=\dfrac{2n+1}{5n-3}\left(n\ne\dfrac{3}{5}\right)\)
Ta có: \(2n+1⋮5n-3\)
\(\Leftrightarrow5.\left(2n+1\right)⋮\left(5n-3\right)\)
\(\Leftrightarrow10n+5⋮5n-3\)
\(\Leftrightarrow2\left(5n-3\right)+11⋮\left(5n-3\right)\)
Vì \(2\left(5n-3\right)⋮\left(5n-3\right)\) nên để D nguyên thì \(11⋮\left(5n-3\right)\)
hay \(5n-3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
`@5n-3=1->n=14/5(l)`
`@5n-3=-1->n=2/5(l)`
`@5n-3=11->n=14/5(l)`
`@5n-3=-11->n=-8/5(l)`
Vậy không có giá trị \(n\in Z\) thỏa mãn

2.24.27+3.19.18+6.57.9
=2.27.24+3.18.19+6.9.57
=54.24+54.19+54.57
=54.(24+19+57)
=54.100 =5400
2.24.27+3.19.18+6.57.9
= 57.24 + 57.18 + 57.9
= 57. ( 24 + 18 + 9 )
= 2907
Study well

9/2-1/2-1+3x=1/2+1/3
=)8/2-1+3x=5/6
=)3+3x=5/6
=)3x=5/6-3
=)3x=13/6
x=13/18
ta có: 9/2 - 1/2 - (1-3x)=1/2 + 1/3
<=>9/2 - 1/2 - (1-3x)=5/6
<=>1/2 - (1-3x) =9/2-5/6
<=>1/2 - (1-3x) =11/3
<=> 1 - 3x = 19/6
<=> 3x =13/6
<=> x =13/18

2\(2x-3\) = 32
2\(2x-3\) = 25
2\(x\) - 3 = 5
2\(x\) = 5 + 3
2\(x\) = 8
\(x\) = 8 : 2
\(x\) = 4

Ta có : \(\left(1\frac{1}{15}\right).\left(1\frac{1}{16}\right).....\left(1\frac{1}{2020}\right)=\frac{16}{15}.\frac{17}{16}....\frac{2021}{2020}=\frac{16.17....2021}{15.16....2020}=\frac{2021}{15}\)

cũng được rồi bạn ạ
Mời bạn tham khảo thêm:
1.2.3.4.5.x với x = -10
Thay x = -10 vào biểu thức ta có :
1.2.3.4.5.(-10)
= (3.4).(2.5).(-10)
= 12.10.(-10)
= 12. (-100)
= - 1200

Ta có \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{2022^2}< \dfrac{1}{2021.2022}\)
cộng vế với vế
\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{2022^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
Vậy ta có đpcm

\(\left[\left(20-2^3.4\right)+\left(3^2.4.16\right)\right]:5\)
\(=\left[\left(-12\right)+576\right]:5\)
\(=564:5=112,8\)
PP/ss: Có thể tính sai ạ ((:
\(\left[\left(20-2^3.4\right)+\left(3^2.4.16\right)\right]:5\)
\(=\left[-12+\left(3^2.4.16\right)\right]:5\)
\(=\left(-12+576\right):5\)
\(=564:5\)
\(=\frac{564}{5}\)


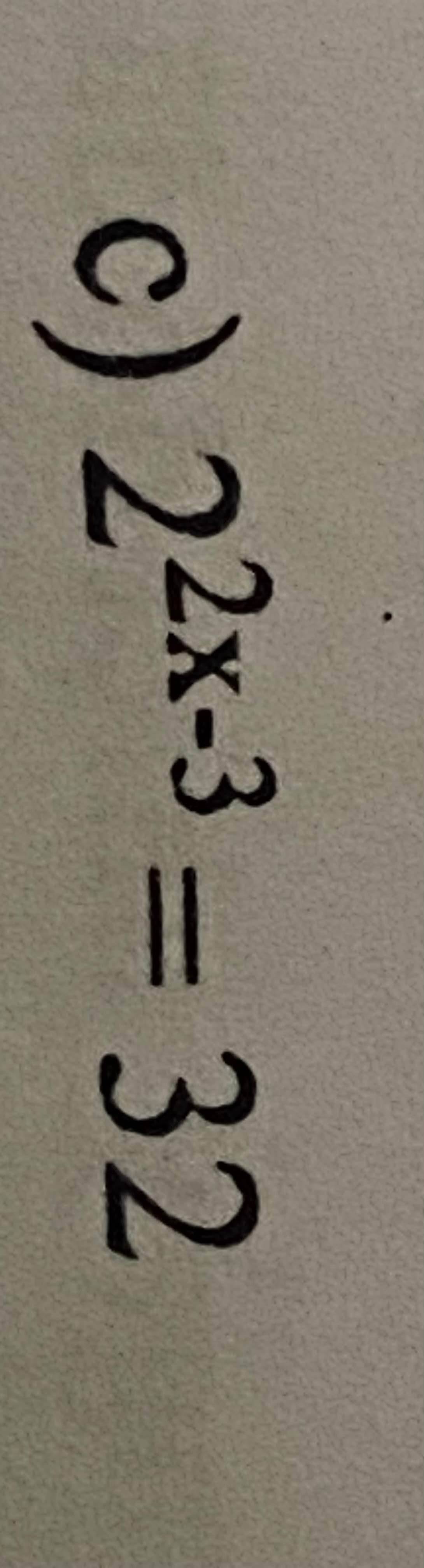
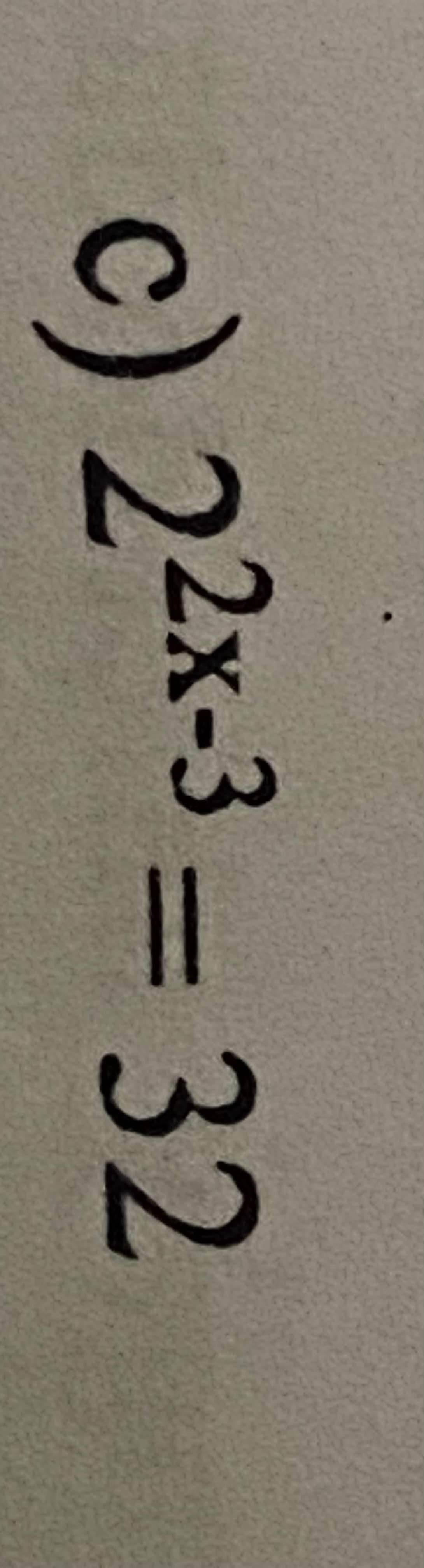
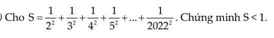
Ta có:
\(A=\frac{5}{n+1}\)là phân số tối giản thì \(n+1\notin5k\left(k\inℤ\right)\)
\(\Rightarrow n=5k-1\left(k\inℤ\right)\)
\(\Rightarrow\)Chọn câu A