K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
G
1
16 tháng 1 2022
a: Xét ΔDOE vuông tại O và ΔKOE vuông tại O có
EO chung
\(\widehat{DEO}=\widehat{KEO}\)
Do đó: ΔDOE=ΔKOE
b: Xét ΔEDI vàΔEKI có
ED=EK
\(\widehat{DEI}=\widehat{KEI}\)
EI chung
Do đó: ΔEDI=ΔEKI
Suy ra: \(\widehat{EDI}=\widehat{EKI}=90^0\)
hay IK\(\perp\)FE
c: Xét ΔDIQ vuông tại D và ΔKIF vuông tại K có
ID=IK
\(\widehat{DIQ}=\widehat{KIF}\)
Do đó: ΔDIQ=ΔKIF
Suy ra: IQ=IF
DT
5
2 tháng 11 2017
Có 2^285 = (2^3)^95 = 8^95
3^190 = (3^2)^95 = 9^95
Vì 8^95 < 9^95 nên 2^285 < 3^190
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 12 2021
\(E=\dfrac{\dfrac{5}{2}\left(2x^2+3\right)+\dfrac{15}{2}}{2x^2+3}=\dfrac{5}{2}+\dfrac{15}{2\left(2x^2+3\right)}\)
Do \(2x^2+3\ge3;\forall x\Rightarrow\dfrac{15}{2\left(2x^2+3\right)}\le\dfrac{15}{2.3}=\dfrac{5}{2}\)
\(\Rightarrow E\le\dfrac{5}{2}+\dfrac{5}{2}=5\)
\(E_{max}=5\) khi \(x=0\)
20 tháng 12 2021
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{24}{8}=3\)
Do đó: x=9; y=15
20 tháng 12 2021
\(d,\Rightarrow-\dfrac{5}{4}x-\dfrac{1}{4}x=-\dfrac{1}{2}-\dfrac{3}{7}\\ \Rightarrow\dfrac{3}{2}x=\dfrac{13}{14}\Rightarrow x=\dfrac{13}{21}\\ e,\Rightarrow7x-7=6x+30\left(x\ne-5\right)\\ \Rightarrow x=37\left(tm\right)\\ f,\Rightarrow\left(27:3\right)^x=9\Rightarrow9^x=9^1\Rightarrow x=1\)
DN
20 tháng 12 2021
d.\(-\dfrac{15}{12}x+\dfrac{3}{7}=\dfrac{1}{4}x-\dfrac{1}{2}\)
\(-\dfrac{3}{2}x=-\dfrac{13}{14}\)
\(x=\dfrac{13}{21}\)
20 tháng 12 2021
\(b,\Rightarrow\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\\ \Rightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\\ c,\Rightarrow\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x-y}{5-2}=\dfrac{15}{3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=25\\y=10\end{matrix}\right.\\ d,\text{Đặt }\dfrac{x}{2}=\dfrac{y}{5}=k\Rightarrow x=2k;y=5k\\ xy=10\Rightarrow10k^2=10\Rightarrow k^2=1\\ \Rightarrow\left[{}\begin{matrix}k=1\\k=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2;y=5\\x=-2;y=-5\end{matrix}\right.\)
\(e,\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2\left(x-1\right)+3\left(y-2\right)-z+3}{2\cdot2+3\cdot3-4}=\dfrac{2x+3y-z-2-6+3}{9}=\dfrac{45}{9}=5\\ \Rightarrow\left\{{}\begin{matrix}x-1=10\\y-2=15\\z-3=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=11\\y=17\\z=23\end{matrix}\right.\)
20 tháng 12 2021
c: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{x-y}{5-2}=5\)
Do đó: x=25; y=10
20 tháng 12 2021
Giải thích các bước giải:
Gọi vận tốc của xe thứ hai là: a (km/h; a > 0)
vận tốc của xe thứ nhất là: 60%a = 35a35a
Gọi thời gian xe thứ nhất đi hết quãng đường AB là: b (h; b > 0)
thời gian xe thứ 2 đi hết quãng đường AB là: b - 3
Vì quãng đường đi như nhau nên thời gian và vận tốc là 2 đại lượng tỉ lệ nghịch ⇒a35a=bb−3=53⇒a35a=bb−3=53
⇒b5=b−33=b−(b−3)5−3=32⇒b5=b−33=b−(b−3)5−3=32 (theo tính chất của dãy tỉ số = nhau)
⇒b=32.5=152=7,5;b−3=7,5−3=4,5⇒b=32.5=152=7,5;b−3=7,5−3=4,5
Vậy thời gian xe thứ nhất đi hết quãng đường AB là 7,5 giờ, thời gian xe thứ 2 đi là 4,5 giờ
?????????????????
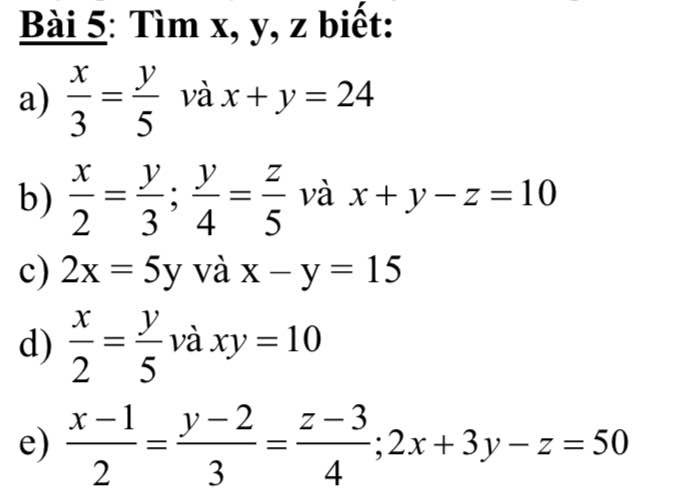
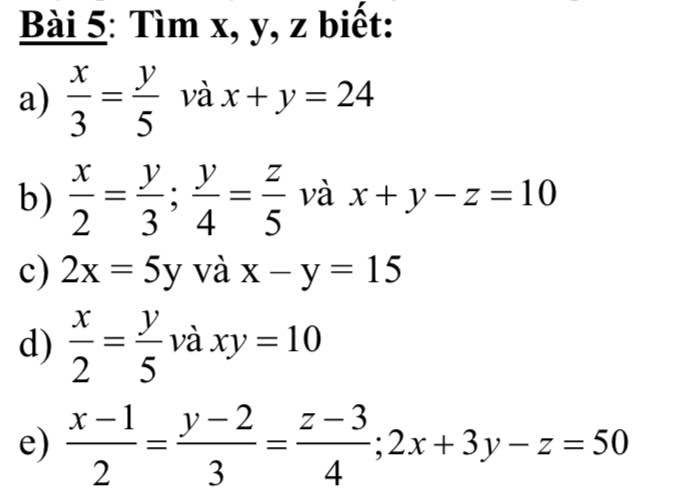
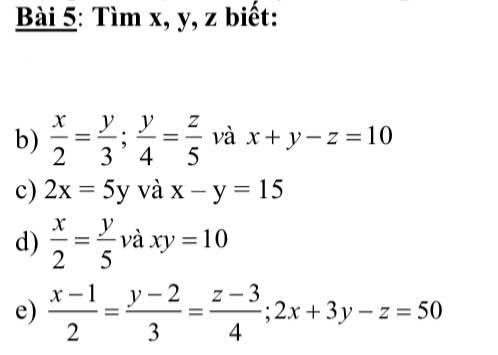