Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath

A B C D M N P Q 1 1 1 1
Có: góc a1+b1= 180-apb
góc c1+d1= 180-cmd
từ 2 cái suy ra a1+b1+c1+d1=360-tổng 2 góc đối(gọi tắt là T2GD nha)
suy ra 360-360/2=T2GD (vì a1=1 nửa góc a, tương tự các cái kia suy ra tổng abcd1 bằng 360/2, tổng các góc trong tg=360)
suy ra 2 góc đối bù nhau
cmtt suy ra 2 góc đối kia cũng bù nhau

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath

Em tham khảo tại link dưới đây nhé:
Câu hỏi của Hoàng Tử Bóng Đêm Kiyoshi - Toán lớp 8 - Học toán với OnlineMath

![[IMG]](http://i.imgur.com/S6gY3so.png)
Tất cả giao điểm được thể hiện trên hình ( vẽ hơi xấu ![]() )
)
Xét ΔADQΔADQ có: MQPˆ=DAQˆ+ADQˆMQP^=DAQ^+ADQ^ (góc ngoài tam giác)
Xét ΔBCNΔBCN có : MNPˆ=BCNˆ+CBNˆMNP^=BCN^+CBN^
⟹MQPˆ+MNPˆ=DAQˆ+ADQˆ+BCNˆ+CBNˆ=1/2(ABCˆ+BCDˆ+CADˆ+DABˆ)=1/2.360o=180o

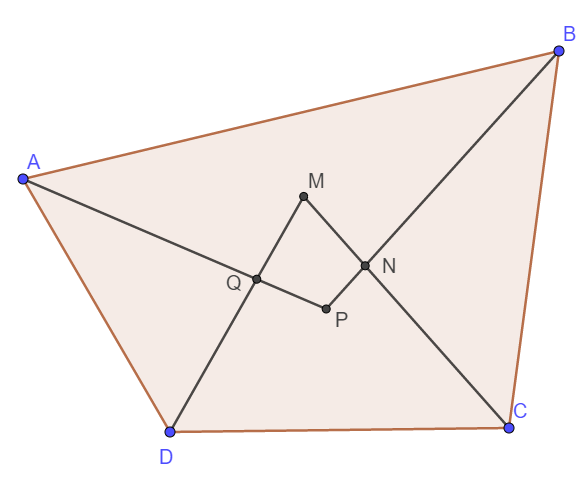
Gọi giao điểm các đường phân giác trong tứ giác ABCD lần lượt là M, N, P, Q như hình vẽ bên trên.
Xét tam giác APB có: \(\widehat{APB}=180^o-\widehat{PAB}-\widehat{PBA}=\frac{360^o-\widehat{DAB}-\widehat{CBA}}{2}\)
Tương tự xét tam giác MCD ta cũng có:
\(\widehat{DMC}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}\)
Suy ra \(\widehat{QMN}+\widehat{QPN}=\frac{360^o-\widehat{ADC}-\widehat{BCD}}{2}+\frac{360^o-\widehat{DAB}-\widehat{ABC}}{2}\)
\(=\frac{720^o-360^o}{2}=180^o\)
Do tổng 4 góc trong một tứ giác bằng 360o nên ta cũng có \(\widehat{MQP}+\widehat{MNP}=360^o-180^o=180^o\)
Vậy tứ giác MNPQ có các góc đối bù nhau.