
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: góc ABC=90 độ-góc ACB
góc KHC=90 độ-góc ACB
=>góc ABC=góc KHC
b: Xét ΔBAH vuông tại A và ΔBKH vuông tại K có
BH chung
góc ABH=góc KBH
=>ΔBAH=ΔBKH
=>BA=BK và HA=HK
=>BH là trung trực của AK
c: Xét ΔIBC có
BD,CA là đường cao
BD căt CAt tại H
=>H là trực tâm
=>I,H,K thẳng hàng
d: ΔADK đều
=>góc ADH=30 độ
=>góc AIK=30 độ
=>góc ABC=60 độ

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{5}{4}}=\dfrac{b}{\dfrac{6}{5}}=\dfrac{c}{\dfrac{11}{10}}=\dfrac{a+b+c}{\dfrac{5}{4}+\dfrac{6}{5}+\dfrac{11}{10}}=\dfrac{710}{\dfrac{71}{20}}=200\)
Do đó: a=250; c=240; c=220


=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ


b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

`B=x^2-9=0`
`-> x^2=0+9`
`-> x^2=9`
`-> x^2=(+-3)^2`
`-> x=+-3`
Vậy, đa thức `B` có `2` nghiệm là `x={3 ; -3}`.

\(\dfrac{x}{9}\) < \(\dfrac{4}{7}\) < \(x\) + \(\dfrac{1}{9}\)
\(\dfrac{7x}{63}\) < \(\dfrac{36}{63}\) < \(\dfrac{63x}{63}\) + \(\dfrac{7}{63}\)
7\(x\) < 36 < 63\(x\) + 7
⇒\(\left\{{}\begin{matrix}7x< 36\\63x+7>36\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>36-7\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>29\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\x>\dfrac{29}{63}\end{matrix}\right.\)
\(\dfrac{29}{63}\)< \(x\) < \(\dfrac{36}{7}\) vì \(x\in\) Z nên \(x\in\) { 1; 2; 3; 4; 5}
⇒ \(\dfrac{x}{9}\) = \(\dfrac{1}{9}\); \(\dfrac{2}{9}\); \(\dfrac{3}{9}\); \(\dfrac{4}{9}\);\(\dfrac{5}{9}\)

\(\dfrac{x}{9}< \dfrac{4}{7}< \dfrac{x+1}{9}\)
=>\(\dfrac{7x}{63}< \dfrac{36}{63}< \dfrac{7x+7}{63}\)
\(\Rightarrow7x< 36< 7x+7\)
\(\Rightarrow x< \dfrac{36}{7}< x+1\)
\(\Rightarrow x< 5\dfrac{1}{7}< x+1\)
\(\Rightarrow x=5\)
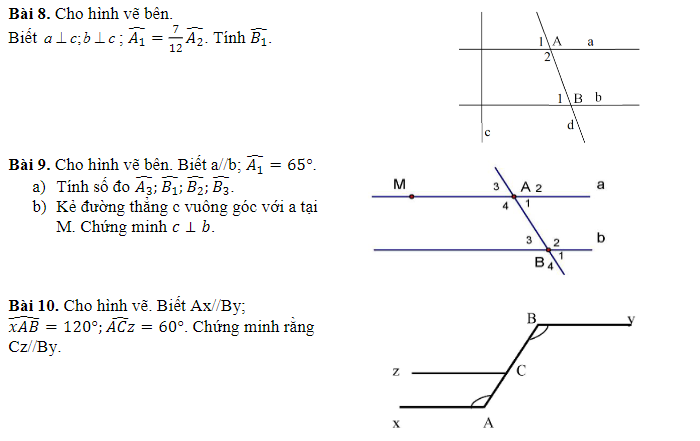


 Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn

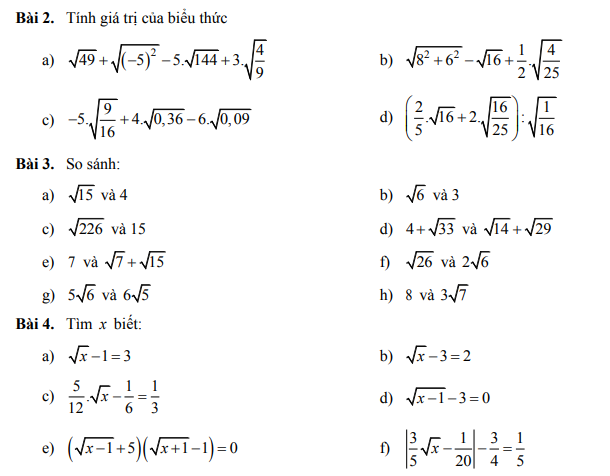 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy