
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)

- AD tính chất định lý talet vào tam giác EPF có MN // FP ta được :
\(\dfrac{EM}{EF}=\dfrac{EN}{EP}=\dfrac{MN}{FP}=\dfrac{12}{x+12}=\dfrac{10}{10+4}=\dfrac{y}{16}\)
\(\Rightarrow\dfrac{12}{x+12}=\dfrac{y}{16}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{80}{7}\\x=\dfrac{24}{5}\end{matrix}\right.\) ( cm )
Vậy ...
Ta có: EP = EN + NP = 10 + 4 = 14 (cm)
Xét tam giác EFP có: MN // FP (gt)
=> \(\dfrac{MN}{FP}=\dfrac{EN}{EP}=\dfrac{EM}{EF}\) (hệ quả định lý Talét)
Thay số: \(\dfrac{y}{16}=\dfrac{10}{14}=\dfrac{12}{12+x}\)
=> \(\left\{{}\begin{matrix}y=\dfrac{80}{7}\\12+x=16,8< =>x=\dfrac{24}{5}\end{matrix}\right.\)

- AD tính chất định lý talet vào tam giác FPQ có MN // PQ ta được :
\(\dfrac{FM}{FQ}=\dfrac{FN}{FP}=\dfrac{MN}{PQ}=\dfrac{10}{y}=\dfrac{12}{16}=\dfrac{x}{20}\)
\(\Rightarrow\dfrac{10}{y}=\dfrac{x}{20}=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}y=\dfrac{40}{3}\\x=15\end{matrix}\right.\) ( cm )
Vậy ...


`2x - 3 = 5`
`<=> 2x = 5 + 3`
`<=> 2x = 8`
`=> x = 4`
Vậy `S = {4}`
_____________________
`3x - 4 = 11`
`<=> 3x = 11 + 4`
`<=> 3x = 15`
`=> x = 5`
Vậy `S = {5}`
______________
`(2x + 1)(x - 3) = 0`
`<=>` $\left[\begin{matrix} 2x + 1 = 0\\ x - 3 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 1/2\\ x = 3\end{matrix}\right.$
Vậy `S = {1/2; -3}`
__________________
`(2x - 3)(x + 2) = 0`
`<=>` $\left[\begin{matrix} 2x - 3 = 0\\ x + 2 = 0\end{matrix}\right.$
`<=>` $\left[\begin{matrix} x = 3/2\\ x = -2\end{matrix}\right.$
Vậy `S = {-2; 3/2}`




a: BC=5cm
=>AM=2,5cm
b: Xet tứ giác AEMF có
góc AEM=góc AFM=góc FAE=90 độ
nên AEMF là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AC
Do đó: E là trung điểm của AB
Xét tứ giác AMBD có
E là trung điểm chung của AB và MD
MA=MB
Do đó: AMBD là hình thoi
 Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)


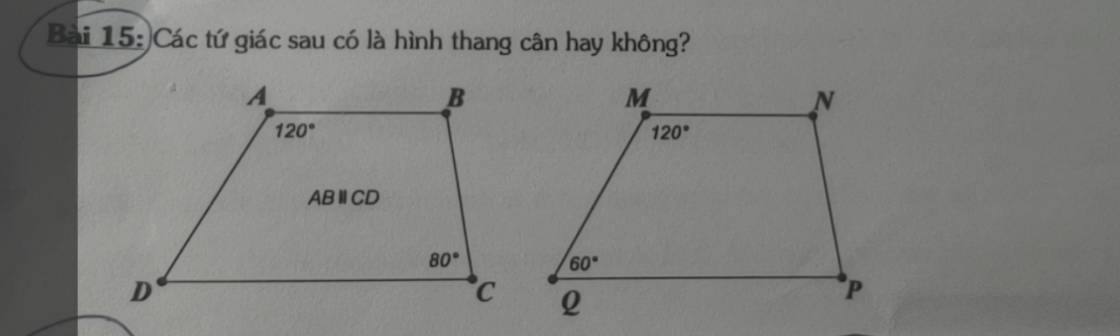
Vẽ tia Ax là tia đối của tia AB
Ta có:
∠xAD + ∠DAB = 180⁰ (kề bù)
⇒ ∠xAD = 180⁰ - ∠DAB
= 180⁰ - 120⁰
= 60⁰
Do AB // CD (gt)
⇒ Ax // CD
⇒ ∠CDA = ∠xAD = 60⁰ (so le trong)
⇒ ∠CDA ≠ ∠BCD (60⁰ 80⁰)
Vậy ABCD không phải hình thang cân
---------------
MNPQ thiếu điều kiện để xét có là hình thang cân hay không rồi em!