K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
giup minh voi
VD
6 tháng 3 2021
ý a,b,c cho 2 tung độ bằng nhau => tính được x1, x2 rồi áp dụng CT diện tích như thường
ý d cũng vậy => tính được x1, x2 nhưng phải xét điều kiện của e^x (x>0)
ý e :
ta có y' = 2x-2 mà M thuộc y' => y' = 4
=> PTTT là: y= 4x-7
xét x^2-2x+2 = 4x-7
=> tính được x1, x2 rồi áp dụng công thức diện tích như 4 ý trên
HN
13 tháng 10 2021
TXĐ: D=R, y'=-x2+10x-26=0 < 0 với mọi x.
Vậy hàm số đã cho nghịch biến trên khoảng (-\(\infty\);+\(\infty\)).
VN
1
9 tháng 3 2016
\(sin 2x-(2sin^2 x-sin2x-2sinx-1/2.\sin 2x+\cos^2x+\cos x-3\sin x-3\cos x+3)=0\)
\(5\sin x.\cos x+5\sin x+2\cos x-\sin^2x-4=0\)
\(\cos x(5\sin x+2)=\sin^2x-5\sin x+4=(\sin x-1)(\sin x -4)\)
Bình phương 2 vế suy ra
\((1-\sin^2 x)(5\sin x+2)^2=(1-\sin x)^2(\sin x-4)^2\)
TH1: \(\sin x=1\)
TH 2: \((1+\sin x)(5\sin x+2)^2=(1-\sin x)(\sin x-4)^2\)
AH
Akai Haruma
Giáo viên
11 tháng 8 2017
Lời giải:
Ta có \(y'=1-m\sin x\). Để hàm số nghịch biến trên R thì \(y'\leq 0\) với mọi \(x\in\mathbb{R}\)
\(\Leftrightarrow 1-m\sin x\leq 0\Leftrightarrow m\sin x\geq 1\)
Nếu \(\sin x=0\) thì hiển nhiên \(m\sin x<1\) nên không tìm được m hợp lý
Nếu đề bài là đồng biến trên R thì bài toán sẽ được giải quyết.
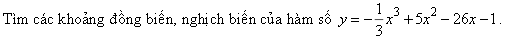
sai nha ban nha