Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(y'=m-3cos3x\)
Hàm đồng biến trên R khi và chỉ khi \(m-3cos3x\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge3cos3x\) ; \(\forall x\)
\(\Leftrightarrow m\ge\max\limits_{x\in R}\left(3cos3x\right)\)
\(\Leftrightarrow m\ge3\)
2.
\(y'=1-m.sinx\)
Hàm đồng biến trên R khi và chỉ khi:
\(1-m.sinx\ge0\) ; \(\forall x\)
\(\Leftrightarrow1\ge m.sinx\) ; \(\forall x\)
- Với \(m=0\) thỏa mãn
- Với \(m< 0\Rightarrow\dfrac{1}{m}\le sinx\Leftrightarrow\dfrac{1}{m}\le\min\limits_R\left(sinx\right)=-1\)
\(\Rightarrow m\ge-1\)
- Với \(m>0\Rightarrow\dfrac{1}{m}\ge sinx\Leftrightarrow\dfrac{1}{m}\ge\max\limits_R\left(sinx\right)=1\)
\(\Rightarrow m\le1\)
Kết hợp lại ta được: \(-1\le m\le1\)

Chọn A
Ta có![]() .
.
![]() .
.
Hàm số ![]() đồng biến trên
đồng biến trên ![]() khi
khi ![]()
![]() .
.
Ta có ![]()
![]() .
.
+TH1 ![]()
![]()
![]()
![]() .
.
+TH2 ![]()
![]()
![]()
![]() .
.
Vậy ![]() .
.

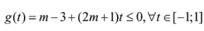
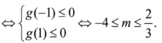
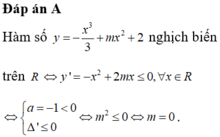
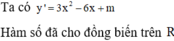
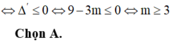

Lời giải:
Ta có \(y'=1-m\sin x\). Để hàm số nghịch biến trên R thì \(y'\leq 0\) với mọi \(x\in\mathbb{R}\)
\(\Leftrightarrow 1-m\sin x\leq 0\Leftrightarrow m\sin x\geq 1\)
Nếu \(\sin x=0\) thì hiển nhiên \(m\sin x<1\) nên không tìm được m hợp lý
Nếu đề bài là đồng biến trên R thì bài toán sẽ được giải quyết.