Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ĐKXĐ: \(x>0\)
\(log_{a^4}x-log_{a^2}x+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{1}{4}log_ax-\frac{1}{2}log_ax+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{3}{4}log_ax=\frac{3}{4}\)
\(\Leftrightarrow log_ax=1\)
\(\Rightarrow x=a\)
Điều kiện xác định : 3\(^x\)>2
Ta có: \(\log_2\left(4.3^x-6\right)=\log_2\left(2\sqrt{2}\right).\log_{2\sqrt{2}}\left(4.3^x-6\right)\)
\(\log_2\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\left(1\right)\)\(\Leftrightarrow\log_2\left(2\sqrt{2}\right)\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)
\(\Rightarrow\dfrac{3}{2}\log_{2\sqrt{2}}\left(4.3^x-6\right)-\dfrac{3}{2}\log_{2\sqrt{2}}\left(9^x-6\right)=1\)\(\Leftrightarrow\dfrac{3}{2}[\log_{2\sqrt{2}}\left(4.3^x-6\right)-\log_{2\sqrt{2}}\left(9^X-6\right)]=1\)
\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\dfrac{2}{3}\)\(\Leftrightarrow\log_{2\sqrt{2}}\left(\dfrac{4.3^X-6}{9^X-6}\right)=\log_{2\sqrt{2}}\left(2\right)\)
\(\Leftrightarrow\dfrac{4.3^X-6}{9^X-6}=2\Leftrightarrow4.3^X-6=2.9^X-12\)\(\Leftrightarrow2.(3^X)^2-4.3^X-6=0\Rightarrow\left[{}\begin{matrix}3^X=3\left(TM\right)\\3^X=-1\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow x=1.\)Vậy x=1 là nghiệm của phương trình (1)
Lời giải:
Đặt \(\log_2x=t\Rightarrow x=2^t\).
Để \(x\in (0;1)\Leftrightarrow 0< 2^t< 1\Leftrightarrow t< 0\)
PT trở thành:
\(t^2+t+m=0\) và ta cần tìm m để pt có nghiệm âm
Điều kiện để pt có nghiệm: \(\Delta=1-4m\geq 0\Leftrightarrow m\leq \frac{1}{4}\) (1)
Áp dụng hệ thức Viete, để PT có nghiệm âm thì:
\(\left\{\begin{matrix} t_1+t_2< 0\\ t_1t_2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} -1< 0\\ m> 0\end{matrix}\right.\Leftrightarrow m> 0\) (2)
Từ (1)(2) suy ra \(0< m\leq \frac{1}{4}\)
\(a^2+4b^2=23ab\Rightarrow a^2+4ab+4b^2=27ab\Rightarrow\left(a+2b\right)^2=27ab\)
\(\Rightarrow\dfrac{\left(a+2b\right)^2}{9}=3ab\)\(\Rightarrow\left(\dfrac{a+2b}{3}\right)^2=3ab\)
Lấy logarit cơ số c hai vế:
\(log_c\left(\dfrac{a+2b}{3}\right)^2=log_c\left(3ab\right)\)
\(\Rightarrow2log_c\dfrac{a+2b}{3}=log_c3+log_ca+log_cb\)
\(\Rightarrow log_c\dfrac{a+2b}{3}=\dfrac{1}{2}\left(log_ca+log_cb+log_c3\right)\)
Lời giải:
Đặt \(\log_9a=\log_{12}b=\log_{16}(a+b)=t\)
\(\left\{\begin{matrix} a=9^t\\ b=12^t\\ a+b=16^t\end{matrix}\right.\Rightarrow 9^t+12^t=16^t\)
Chia 2 vế cho \(12^t\) ta có:
\(\left(\frac{9}{12}\right)^t+1=\left(\frac{16}{12}\right)^t\)
\(\Leftrightarrow \left(\frac{3}{4}\right)^t+1=\left(\frac{4}{3}\right)^t\) (1)
Đặt \(\frac{a}{b}=\left(\frac{9}{12}\right)^t=\left(\frac{3}{4}\right)^t=k\). Thay vào (1):
\(k+1=\frac{1}{k}\Leftrightarrow k^2+k-1=0\)
\(\Leftrightarrow \frac{a}{b}=k=\frac{-1+ \sqrt{5}}{2}\) (do \(k>0\) nên loại TH \(k=\frac{-1-\sqrt{5}}{2}\) )
Thấy \(\frac{-1+\sqrt{5}}{2}\in (0;\frac{2}{3})\) nên chọn đáp án b
Lời giải:
Đặt \(\log_{\frac{1}{2}}\sqrt{x+1}=t\Rightarrow \sqrt{x+1}=(\frac{1}{2})^t\)
\(\Rightarrow x+1=(\frac{1}{2})^{2t}=(2^{-1})^{2t}=2^{-2t}\)
\(\Rightarrow \log_2(x+1)=-2t\)
Vậy pt ban đầu tương đương với:
\(-2t+t=1\Leftrightarrow t=-1\)
\(\Rightarrow x+1=2^{-2t}=4\Rightarrow x=3\)
Chọn D.
Phương trình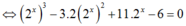
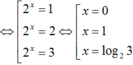thỏa mãn (*)
Do đó S = 1+ log23 = log26.