Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trình bày công thức các thứ khá dài nên tôi thử nói hướng, nếu bạn hiểu đc và làm đc thì ok còn nếu k hiểu thì bảo mình, mình làm full cho
Bây giờ phân tích mẫu trước, ra (x-1)2(x+2)
Để cái lim này nó ra đc 1 số thực thì tử và mẫu cùng phải triệt tiêu (x-1)2 đi, tức là tử phải chia hết (x-1)2, tức là tử cũng phải có nghiệm kép x=1
Do đó \(\left\{{}\begin{matrix}f\left(1\right)=0\\f'\left(1\right)=0\end{matrix}\right.\)

Giới hạn đã cho hữu hạn khi \(\sqrt{ax+b}-3=0\) có nghiệm \(x=3\)
\(\Rightarrow\sqrt{3a+b}=3\Rightarrow3a+b=9\Rightarrow b=9-3a\)
\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{ax+9-3a}-3}{3\left(9-x^2\right)}=\lim\limits_{x\rightarrow3}\dfrac{a\left(x-3\right)}{-3\left(x+3\right)\left(x-3\right)\left(\sqrt{ax+9-3a}+3\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{-a}{3\left(x+3\right)\left(\sqrt{ax+9-3a}+3\right)}=\dfrac{-a}{18.6}=\dfrac{1}{54}\Rightarrow a=-2\)
\(\Rightarrow b=15\)

\(\sqrt{a+12}-\sqrt[3]{81+63-19}=0\Rightarrow a=13\)
Khi đó
\(\dfrac{\sqrt{13x^2+4x+8}-\sqrt[3]{81x^2+63x-19}}{\left(x-1\right)^2\left(x+1\right)}\)
\(=\dfrac{\sqrt[]{13x^2+4x+8}-\left(3x+2\right)+\left(3x+2-\sqrt[3]{81x^2+83x-19}\right)}{\left(x-1\right)^2\left(x+1\right)}\)
\(=\dfrac{\dfrac{4\left(x-1\right)^2}{\sqrt[]{13x^2+4x+8}+\left(3x+2\right)}+\dfrac{27\left(x-1\right)^2\left(x+1\right)}{\left(3x+2\right)^2+\left(3x+2\right)\sqrt[3]{81x^2+63x-19}+\sqrt[3]{\left(81x^2+63x-19\right)^2}}}{\left(x-1\right)^2\left(x+1\right)}\)

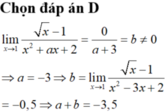


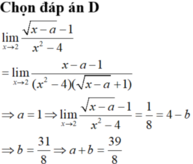
Vì b \(\ne\) 0 nên tồn tại f(x) sao cho:
\(x^2+ax+2=\left(x-1\right).f\left(x\right)\)
=> 1 + a + 2 = 0
=> a = -3; f(x) = x - 2
Khi đó:
\(\lim\limits_{x\rightarrow1}\frac{x-1}{\left(\sqrt{x}+1\right)\left(x-1\right)f\left(x\right)}=b\)
\(\Leftrightarrow\lim\limits_{x\rightarrow1}\frac{1}{\left(\sqrt{x}+1\right)f\left(x\right)}=b\)
\(\Leftrightarrow b=\lim\limits_{x\rightarrow1}\frac{1}{\left(\sqrt{x}+1\right)\left(x-2\right)}=\frac{1}{2.\left(-1\right)}=-\frac{1}{2}\)
tks b !!!