Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(\lim\limits_{x\rightarrow0}\dfrac{2\sqrt{1+x}-2+2-\sqrt[3]{8-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{2x}{\sqrt{1+x}+1}+\dfrac{x}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{2}{\sqrt{1+x}+1}+\dfrac{1}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}\right)=\dfrac{13}{12}\)
2/ \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-\sqrt{x+3}}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2-\left(\sqrt{x+3}-2\right)}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{x-1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}-\dfrac{x-1}{\sqrt{x+3}+2}}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}-\dfrac{1}{\sqrt{x+3}+2}}{x-2}=\dfrac{1}{6}\)
3/ \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^2+7}-\sqrt{5-x^2}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^2+7}-2+2-\sqrt{5-x^2}}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{\left(x^2-1\right)}{\sqrt[3]{\left(x^2+7\right)^2}+2\sqrt[3]{x^2+7}+4}+\dfrac{x^2-1}{2+\sqrt{5-x^2}}}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\dfrac{1}{\sqrt[3]{\left(x^2+7\right)^2}+2\sqrt[3]{x^2+7}+4}+\dfrac{1}{2+\sqrt{5-x^2}}\right)=\dfrac{1}{3}\)
4/ \(\lim\limits_{x\rightarrow-2}\dfrac{\sqrt{x+11}-\sqrt[3]{8x+43}}{2x^2+3x-2}=\lim\limits_{x\rightarrow-2}\dfrac{\sqrt{x+11}-3-\left(\sqrt[3]{8x+43}-3\right)}{\left(2x-1\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow-2}\dfrac{\dfrac{x+2}{\sqrt{x+11}+3}-\dfrac{8\left(x+2\right)}{\sqrt[3]{\left(8x+43\right)^2}+3\sqrt[3]{8x+43}+9}}{\left(2x-1\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow-2}\dfrac{\dfrac{1}{\sqrt{x+11}+3}-\dfrac{8}{\sqrt[3]{\left(8x+43\right)^2}+3\sqrt[3]{8x+43}+9}}{2x-1}=\dfrac{7}{270}\)
5/ \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt[n]{1+ax}-\sqrt[m]{1+bx}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\sqrt[n]{1+ax}-1-\left(\sqrt[m]{1+bx}-1\right)}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{ax}{\sqrt[n]{\left(1+ax\right)^{n-1}}+\sqrt[n]{\left(1+ax\right)^{n-2}}+...+1}-\dfrac{bx}{\sqrt[m]{\left(1+bx\right)^{m-1}}+\sqrt[m]{\left(1+ax\right)^{m-2}}+...+1}}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(1+ax\right)^{n-1}}+\sqrt[n]{\left(1+ax\right)^{n-2}}+...+1}-\dfrac{b}{\sqrt[m]{\left(1+bx\right)^{m-1}}+\sqrt[m]{\left(1+ax\right)^{m-2}}+...+1}\)
\(=\dfrac{a}{n}-\dfrac{b}{m}\)
6/ \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\sqrt[3]{1+6x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\sqrt[3]{1+6x}-\sqrt{1+4x}+\sqrt{1+4x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\left(\sqrt[3]{1+6x}-1\right)+\sqrt{1+4x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\dfrac{6x}{\sqrt[3]{\left(1+6x\right)^2}+\sqrt[3]{1+6x}+1}+\dfrac{4x}{\sqrt{1+4x}+1}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{6\sqrt{1+4x}}{\sqrt[3]{\left(1+6x\right)^2}+\sqrt[3]{1+6x}+1}+\dfrac{4}{\sqrt{1+4x}+1}\right)=4\)

Đặt \(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+....+\frac{1}{n\left(n+1\right)}=A\)
\(\Leftrightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{n}-\frac{1}{n+1}\)
\(\Leftrightarrow A=\frac{n+1}{n+1}-\frac{1}{n+1}=\frac{n}{n+1}\)

\(\frac{\sqrt{ax+1}\left(\sqrt[3]{bx+1}-1\right)+\sqrt{ax+1}-1}{x}=\frac{\frac{bx\sqrt{ax+1}}{\sqrt[3]{\left(bx+1\right)^2}+\sqrt[3]{bx+1}+1}+\frac{ax}{\sqrt{ax+1}+1}}{x}=\frac{b\sqrt{ax+1}}{\sqrt[3]{\left(bx+1\right)^2}+\sqrt[3]{bx+1}+1}+\frac{a}{\sqrt{ax+1}+1}\)
\(\Rightarrow\lim\limits_{x\rightarrow0}f\left(x\right)=a+b\Rightarrow a+b=1\)
\(a^2+b^2\ge\frac{1}{2}\left(a+b\right)^2=\frac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=\frac{1}{2}\)
Mình sử dụng L'Hopital nhé, 2 loại căn thế này tìm liên hợp kép dài lắm :D
\(\lim\limits_{x\rightarrow1}\frac{\left(6x-5\right)^{\frac{1}{3}}-\left(4x-3\right)^{\frac{1}{2}}}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\frac{2\left(6x-5\right)^{-\frac{2}{3}}-2\left(4x-3\right)^{-\frac{1}{2}}}{2\left(x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{-4\left(6x-5\right)^{-\frac{5}{3}}+2\left(4x-3\right)^{-\frac{3}{2}}}{1}=-2\)
Nếu ko bạn tách liên hợp như vầy:
\(\frac{\left(\sqrt[3]{6x-5}-2x+1\right)+\left(2x-1-\sqrt{4x-3}\right)}{\left(x-1\right)^2}\)
Sẽ khử được \(\left(x-1\right)^2\)
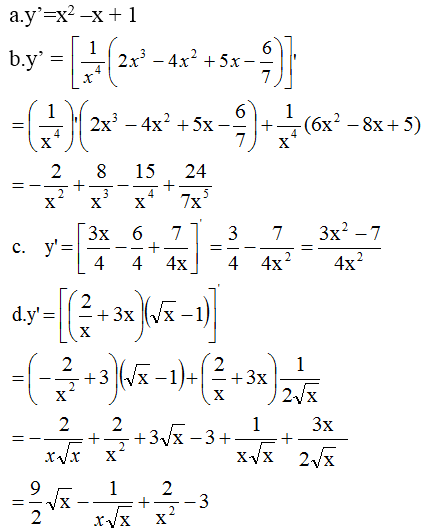
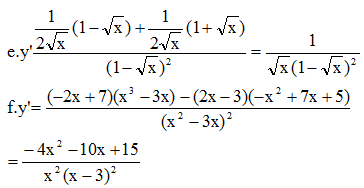
Giới hạn đã cho hữu hạn khi \(\sqrt{ax+b}-3=0\) có nghiệm \(x=3\)
\(\Rightarrow\sqrt{3a+b}=3\Rightarrow3a+b=9\Rightarrow b=9-3a\)
\(\lim\limits_{x\rightarrow3}\dfrac{\sqrt{ax+9-3a}-3}{3\left(9-x^2\right)}=\lim\limits_{x\rightarrow3}\dfrac{a\left(x-3\right)}{-3\left(x+3\right)\left(x-3\right)\left(\sqrt{ax+9-3a}+3\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{-a}{3\left(x+3\right)\left(\sqrt{ax+9-3a}+3\right)}=\dfrac{-a}{18.6}=\dfrac{1}{54}\Rightarrow a=-2\)
\(\Rightarrow b=15\)