Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Không biết bạn nhận được nguồn tin từ mới nào mà cho là không có giải vậy nhỉ? Hay là bạn chưa bao giờ được nhận nên nói vậy? Anh hùng bàn phím bay giờ cũng phải chịu trách nhiệm trước pháp luật đấy bạn nhé!
không đăng câu hỏi linh tinh
100% không có giải
lợi dụng đó mọi người đừng tin

Không gian mẫu là chọn ngẫu nhiên 5 học sinh từ 12 học sinh.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 5 học sinh được chọn có 3 học sinh nam và 2 học sinh nữ trong đó phải nhất thiết có bạn An hoặc bạn Hoa nhưng không có cả hai . Ta mô tả các trường hợp thuận lợi cho biến cố A như sau:
● Trường hợp 1. Có bạn An.
Chọn thêm 2 học sinh nam từ 6 học sinh nam, có ![]() cách.
cách.
Chọn 2 học sinh nữ từ 4 học sinh nữ (không chọn Hoa), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Có bạn Hoa.
Chọn thêm 1 học sinh nữ từ 4 học sinh nam, có ![]() cách.
cách.
Chọn 3 học sinh nam từ 6 học sinh nam (không chọn An), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố là ![]()
Vậy xác suất cần tính 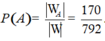
Chọn C.

Đây cũng là một ý tưởng hay đó em ah. Chúc các em phát triển nhóm và cùng giúp nhau trong cuộc sống, sẽ chia và giúp đỡ nhau cùng tiến bộ. Thân mến!

Hàm tuần hoàn chu kì \(T=2\pi\) nên ta chỉ cần khảo sát trên đoạn \(\left[0;2\pi\right]\)
\(y'=-3cosx-4sin2x=0\Leftrightarrow-cosx\left(3+8sinx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arcsin\left(-\frac{3}{8}\right)+k2\pi\\x=\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\end{matrix}\right.\)
Để ngắn gọn thì đặt \(b=2\pi+arcsin\left(-\frac{3}{8}\right)\) ; \(a=\pi-arcsin\left(-\frac{3}{8}\right)\)
BBT:

Hàm đạt cực tiểu tại \(x=\frac{\pi}{2}+k\pi\)
Hàm đạt cực đại tại \(\left[{}\begin{matrix}x=arcsin\left(-\frac{3}{8}\right)+k2\pi\\x=\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(\frac{\pi}{2}+k2\pi;\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi\right)\) và \(\left(\frac{3\pi}{2}+k2\pi;arcsin\left(-\frac{3}{8}\right)+k2\pi\right)\)
Hàm nghịch biến trên các khoảng \(\left(\pi-arcsin\left(-\frac{3}{8}\right)+k2\pi;\frac{3\pi}{2}+k2\pi\right)\) và \(\left(arcsin\left(-\frac{3}{8}\right)+k2\pi;\frac{5\pi}{2}+k2\pi\right)\)
\(y_{max}=\frac{89}{16}\) khi \(sinx=-\frac{3}{8}\)
\(y_{min}=-2\) khi \(sinx=1\)


