K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
14 tháng 8 2023
4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1
KV
31 tháng 10 2023
Bài 1
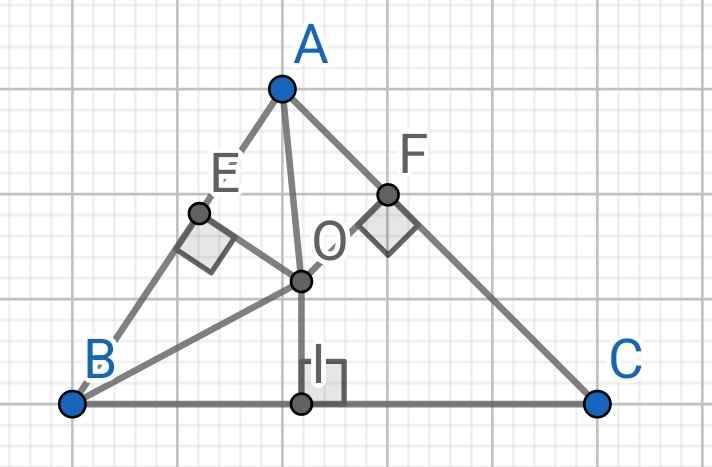Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
KV
31 tháng 10 2023
Bài 2
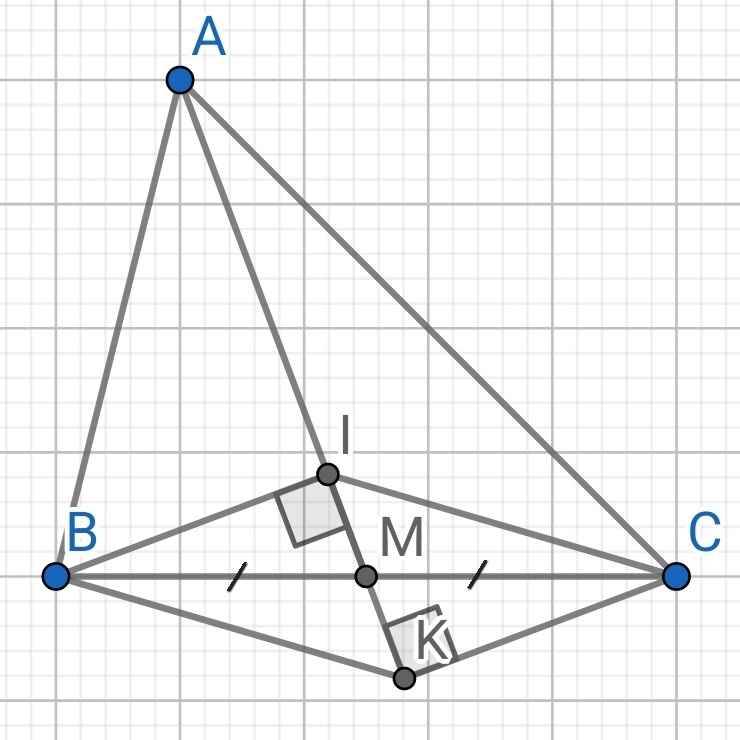a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI
TN
1
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
NT
0
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
Xét tam giác $ABM$ và $ACM$ có:
$AB=AC$ (gt)
$BM=CM$ (do $M$ là trung điểm $BC$)
$AM$ chung
$\Rightarrow \triangle ABM=\triangle ACM$ (c.c.c)
T
0
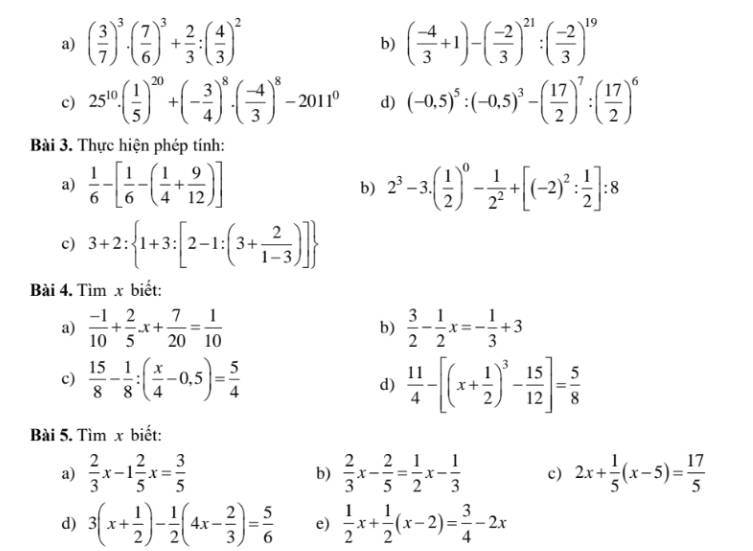
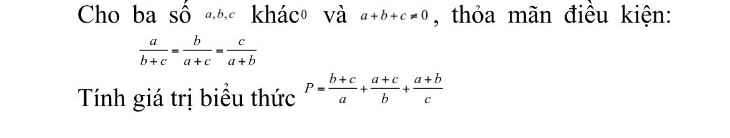
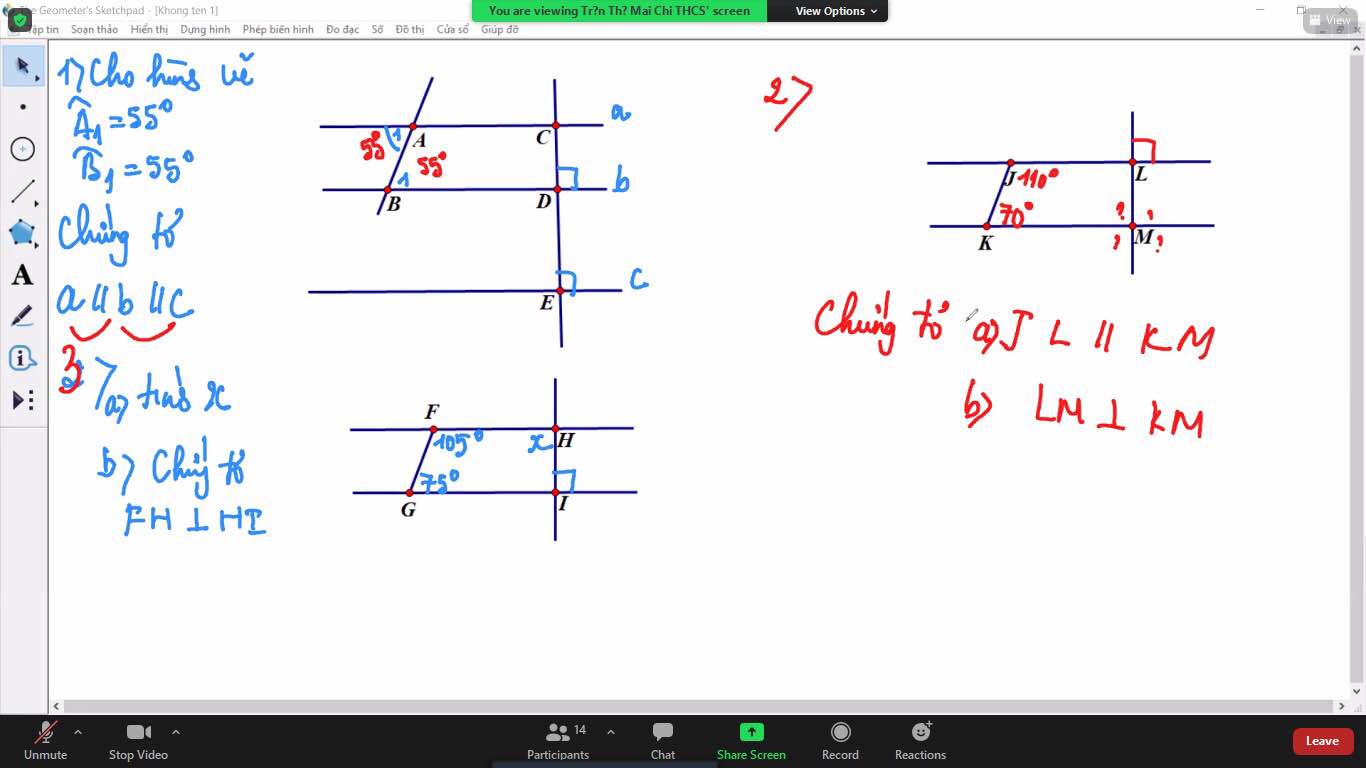
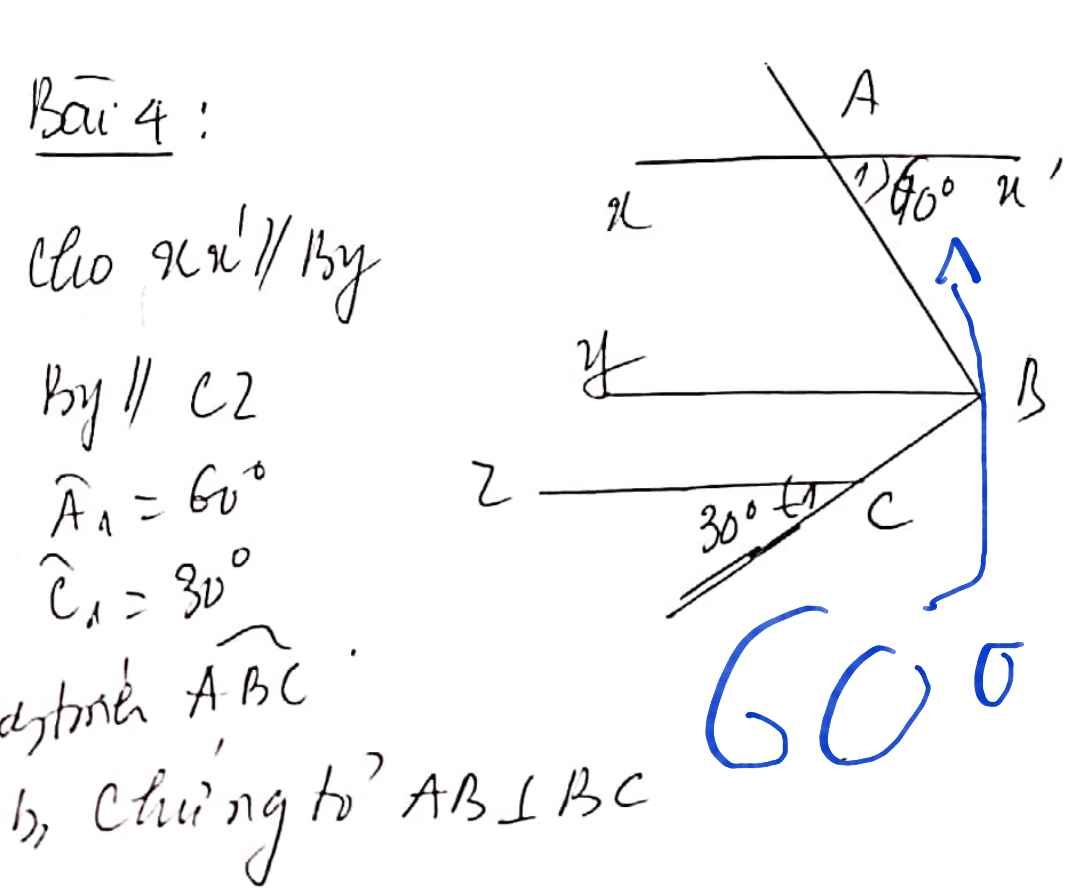
Đây nhé
a, 3 (10x) = 111
30x = 111
x = 111/30
b, 3 (10 + x) = 111
30 + 3x = 111
3x = 111 - 30
3x = 81
x = 81
x = 27
c, 3 + (10x) = 111
10x = 111 - 3
10x = 108
x = 108 : 10
x = 10,8
d, 3 + (10 + x) = 111
3 + 10 + x = 111
13 + x = 111
x = 111 - 13
x = 98
a, 30x = 111
x = 111/30
b, 30 + 3x = 111
3x = 81
x = 27
c, 10x = 108
x = 10,8
d, 13 + x = 111
x = 98