Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

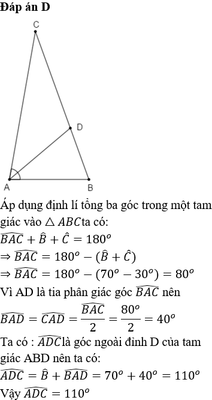
Tam giác ABC có:
góc BAC + góc B + góc C = 180 độ
=> góc BAC + 80 độ + 30 độ = 180 độ
=> góc BAC = 180 độ - ( 80 độ + 30 độ) =70 độ
Vì AD là tia phân giác của góc BAC nên:
góc BAD = góc BAC / 2 = 70/2 = 35 độ
Vì góc ADC là góc ngoài của tam giác ADB nên:
góc ADC = góc B + góc BAD
= 80 độ + 35 độ =115 độ
Ta có: góc ADB + góc ADC = 180 độ ( kề bù)
=> góc ADB = 180 độ - góc ADC
= 180 độ - 115 độ = 65 độ
Vậy góc ADC = 115 độ, góc ADB = 65 độ
chúc em học tốt !

Vẽ hình:
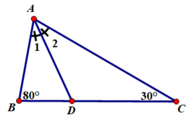

Áp dụng định lý góc ngoài trong các tam giác ABD và ACD ta có:
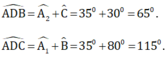

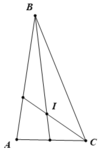
b. Khi ∠B = 30o thì ∠C = 180o - 30o - 80o = 70o ( 1 điểm )
Vì ∠B < ∠C < ∠A ⇒ AC < AB < BC ( 1 điểm )

a: ΔABC cân tại A
=>\(\hat{ABC}=\hat{ACB}\)
=>\(\hat{ACB}=80^0\)
ΔABC cân tại A
=>\(\hat{BAC}=180^0-2\cdot\hat{ABC}=180^0-2\cdot80^0=20^0\)
Ta có: \(\hat{IAC}=\frac12\cdot\hat{BAC}\left(10^0=\frac12\cdot20^0\right)\)
=>AI là phân giác của góc BAC
Ta có: \(\hat{ACI}+\hat{ICB}=\hat{ACB}\) (tia CI nằm giữa hai tia CA và CB)
=>\(\hat{ICB}=80^0-30^0=50^0\)
Xét ΔAIC có \(\hat{AIC}+\hat{IAC}+\hat{ICA}=180^0\)
=>\(\hat{AIC}=180^0-30^0-10^0=140^0\)
Xét ΔAIB và ΔAIC có
AI chung
\(\hat{BAI}=\hat{CAI}\)
AB=AC
Do đó: ΔAIB=ΔAIC
=>\(\hat{AIB}=\hat{AIC}=140^0\)
b: AI là phân giác của góc BAC
=>\(\hat{BAI}=\hat{CAI}=\frac12\cdot\hat{BAC}=10^0\)
AK là phân giác của góc BAI
=>\(\hat{BAK}=\hat{KAI}=\frac12\cdot\hat{BAI}=5^0\)
\(\hat{KAC}=\hat{KAI}+\hat{IAC}=5^0+10^0=15^0\)
Vì I nằm trên tia KC
nên \(\hat{KCA}=\hat{ICA}\)
=>\(\hat{KCA}=30^0\)

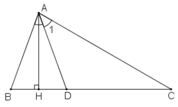
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o

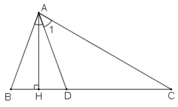
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o

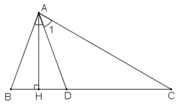
Trong ΔABC có:
∠(BAC) + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Mà ∠(BAC) + 70o + 30o = 180
Vậy ∠(BAC) = 180o-70o - 30o = 80o