Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\hept{\begin{cases}\widehat{HFE}=\widehat{HAE}\\\widehat{HAE}+\widehat{ABH}=90^O\end{cases}\Rightarrow\widehat{HFE}+\widehat{ABH}=90^O}\)
=> \(\widehat{HFE}+\widehat{ABC}=90^O\)(đpcm)
b) AEHF nội tiếp => \(\widehat{AEF}=\widehat{AHF}\)
Mà \(\widehat{AHF}=\widehat{ACB}\)( cùng phụ với \(\widehat{HAC}\))
=> \(\widehat{AEF}=\widehat{ACB}\)
=> BEFC là tứ giác nội tiếp
\(\Rightarrow\hept{\begin{cases}\widehat{EBF}=\widehat{FCE}\\\widehat{BEM}=\widehat{NFC}=90^O\end{cases}\Rightarrow\widehat{EMB}=\widehat{FNC}}\)
\(\Rightarrow\widehat{EMF}=\widehat{ENF}\)
=> EMNF là tứ giác nội tiếp
=> góc ENM = góc EFB
Mà BEFC nội tiếp => góc EFB = góc ECB
Từ 2 điều trên => góc ENM = góc ECB
=> MN // BC => đpcm

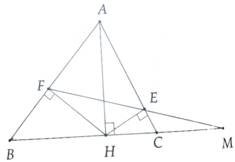
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
hay BC=15cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC,ta được:
\(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=7,2\left(cm\right)\\BH=5,4\left(cm\right)\\CH=9,6\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HB\cdot HC=AE\cdot AB\)

a: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp
\(\frac{1}{2}BF.AH.sinBIH=\frac{1}{2}\left(BI+IF\right)\left(AI+IH\right)sinBIH\)
\(=\frac{1}{2}\left(BI.AI+BI.IH+IF.AI+IF.IH\right).sinBIH\)
\(=\frac{1}{2}BI.AI.sinBIH+\frac{1}{2}BI.IH.sinBIH+\frac{1}{2}IF.AI.sinBIH+\frac{1}{2}IF.IH.sinBIH\)
\(=S_{AIB}+S_{BIH}+S_{AIF}+S_{FIH}=S_{FABH}\)