Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thêm nữa câu a) Tính: M(x) + N(x)+ P(x)
B) Tính M(x) - N (x) - P(x)
ok rồi giúp mình với nha

a,(\(6x-5x^2-15+2x^3:\left(2x-5\right)\)
\(\left(2x^3-5x^2+6x-15\right):\left(2x-5\right)\)
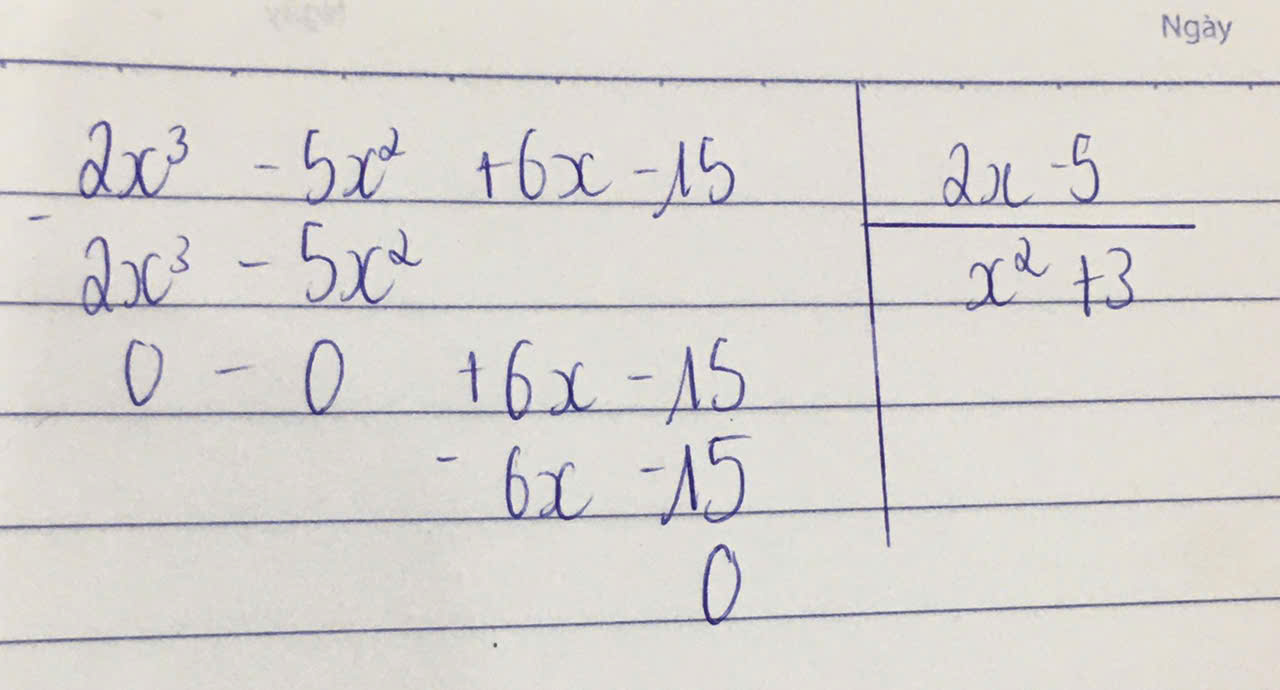

a. x = {3;-3}
b. x thuộc rỗng
c. x2-4=0
x2 = 4
x={2;-2}
d. x2+1=82
x2 =83
x thuộc rỗng
e. (2x)2=6
x thuộc rỗng
f. (x-1)2=9
TH1: x-1=3=>x=4
TH2: x-1=-3=>x=-2
Vậy x={4;-2}
g.(2x+3)2=25
TH1: 2x+3=5=> x=1
Th2: 2x+3=-5=>x=-4
VẬY X={1;-4}
a, x^2= 9
=>\(\sqrt{9}=3\)
b,\(x^2=5=>x=\sqrt{5}\)
c, x^2-4=0
=>x^2=4
=>x=2
d, x^2+1=82
=>x^2=81 =>\(\sqrt{81}=9\)
3, 2x^2=6
=>x= \(\sqrt{6}\)
f, {x-1} ^2=9
=> x-1=3
=>x=2
g{ 2x+3}^2=25
=> 2x+3=5
=>2x=2
=>x=1

a) x^2 = 9 => x=3 hoặc x = -3
b) x^2 = 5 => \(x=\sqrt{5}\)
c) x^2 - 4 = 0
=> x^2 = 4 => x = 2 hoặc x = -2
d) x^2 + 1 = 82
=> x^2 = 81 => x = 9 hoặc x = -9
e) (2x)^2 = 6
=> 4 . x^2 = 6
=> x^2 = 3/2
=> \(x=\sqrt{\frac{3}{2}}\)
f) (x-1)^2 = 9
=> x-1 = 3 hoặc x - 1 = -3
=> x = 4 hoặc -2
g) (2x+3)^2 = 25
=> 2x + 3 = 5 hoặc 2x + 3 = -5
=> x = 1 hoặc x = -4
Ta có:
a, \(x^2=9\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)
b, \(x^2=5\Rightarrow\orbr{\begin{cases}x=2,5\\x=-2.5\end{cases}}\)
Các câu còn lại tương tự nhé bn

a)3^x+1=9^x
3^x+1=3.3^x
3^x+1=3^x+1
=>x thuộc TH Z
b)2^3.x+2=4^x+5
2^3x+2=2^2.(x+5)
2^3x+2=2^2x+10
2^3x=2^2x+8
3x-2x=8
=>x=8
c)3^2x-1=243
3^2x=243.3
3^2x=729
3^2x=3^6
=>2x=6
x=6:2=3
chúc bạn học tốt nha

\(4)D=x^2+x+1\)
\(D=x^2+2x.\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1\)
\(D=\left(x+\frac{1}{2}\right)^2-\frac{1}{4}+1\)
\(D=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
Vậy biểu thức trên luôn nhận giá trị dương với mọi giá trị của x.
Các câu khác lm tương tự nhé.
Cho góp ý xíu: lần sau bn đưa từng câu một lên diễn đàn thì sẽ có câu trả lời nhanh hơn là đưa cùng một lúc như thế này đấy
hok tốt~
\(D=x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\left(x+\frac{1}{2}\right)^2\ge0\forall x\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)( đpcm )
\(F=2x^2+4x+3=2\left(x^2+2x+1\right)+1=2\left(x+1\right)^2+1\)
\(2\left(x+1\right)^2\ge0\forall x\Rightarrow2\left(x+1\right)^2+1\ge1>0\forall x\)( đpcm )
\(G=3x^2-5x+3=3\left(x^2-\frac{5}{3}x+\frac{25}{36}\right)+\frac{11}{12}=3\left(x-\frac{5}{6}\right)^2+\frac{11}{12}\)
\(3\left(x-\frac{5}{6}\right)^2\ge0\forall x\Rightarrow3\left(x-\frac{5}{6}\right)^2+\frac{11}{12}\ge\frac{11}{12}>0\forall x\)( đpcm )
\(H=4x^2+4x+2=4\left(x^2+x+\frac{1}{4}\right)+1=4\left(x+\frac{1}{2}\right)^2+1\)
\(4\left(x+\frac{1}{2}\right)^2\ge0\forall x\Rightarrow4\left(x+\frac{1}{2}\right)^2+1\ge1>0\forall x\)( đpcm )
\(K=4x^2+3x+2=4\left(x^2+\frac{3}{4}x+\frac{9}{64}\right)+\frac{23}{16}=4\left(x+\frac{3}{8}\right)^2+\frac{23}{16}\)
\(4\left(x+\frac{3}{8}\right)^2\ge0\forall x\Rightarrow4\left(x+\frac{3}{8}\right)^2+\frac{23}{16}\ge\frac{23}{16}>0\forall x\)( đpcm )
\(L=2x^2+3x+4=2\left(x^2+\frac{3}{2}x+\frac{9}{16}\right)+\frac{23}{8}=2\left(x+\frac{3}{4}\right)^2+\frac{23}{8}\)
\(2\left(x+\frac{3}{4}\right)^2\ge0\forall x\Rightarrow2\left(x+\frac{3}{4}\right)^2+\frac{23}{8}\ge\frac{23}{8}>0\forall x\)( đpcm )
a: =>9(2x+1)=6(3-x)
=>3(2x+1)=2(3-x)
=>6x+3=6-2x
=>8x=3
=>x=3/8
b: =>-3x^2-2+3x^2-18x=-26
=>-18x=-24
=>x=4/3