Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ABC vuông tại A có \(BC^2=AB^2+AC^2\left(pytagor\right)\)
\(\Rightarrow BC=10\left(cm\right)\)
xét tam giác ABC ta có AD là đường phân giác => \(\frac{BD}{AB}=\frac{DC}{AC}=\frac{BC}{AB+AC}=\frac{5}{7}\)
=> BD= 30/7 (cm) ; DC= 40/7 (cm)
b/ có DH vuông góc AB ; AC vuông góc AB (tam giác vuông)
=> DH//AC => \(\frac{DH}{AC}=\frac{BD}{BC}=\frac{BH}{AB}\)(hệ quả Thales) => \(DH=\frac{AC.BD}{BC}=\frac{24}{7}\left(cm\right)\)
ta có HAD=CAD (p/giác) ; HDA=CAD( 2 góc slt; DH//AC) => HAD=HDA => tam giác AHD cân tại H
mà tam giác AHD vuông tại H => tam giác AHD vuông cân tại H
=> \(AD^2=2DH^2\)=> \(AD=\frac{24\sqrt{2}}{7}\left(cm\right)\)
mình ko tính ra số thập phân. Bạn tự tính nhé. Chúc bn học tốt

1: Xét ΔABC có BD là đường phân giác
nên AD/CD=AB/BC=3/5
2: Xét ΔCHD vuông tại H và ΔCAB vuông tại A có
\(\widehat{C}\) chung
do đó: ΔCHD∼ΔCAB
Suy ra: HD/AB=CD/CB
hay \(CD\cdot AB=HD\cdot CB\)

Áp dụng Pitago ta có : BC = 10
Áp dụng tính chất của tia phân giác ta có : BD/DC = AB/AC = 3/4
=> BD/BC = 3/7 => BD = 30/7 cm, CD = 40/7 cm
HD // AC => HD / AC = BD / BC
=> HD = 30/70.8 = 24/7
Do góc HAD = 45 độ => T/g HAD vuông cân => AD^2 = 1152/49 => AD = \(\frac{24\sqrt{2}}{7}\)cm

a: AD/CD=BA/CB=3/5
b: ΔBAD đồng dạng với ΔBHD
ΔCHD đồng dạng với ΔCAB

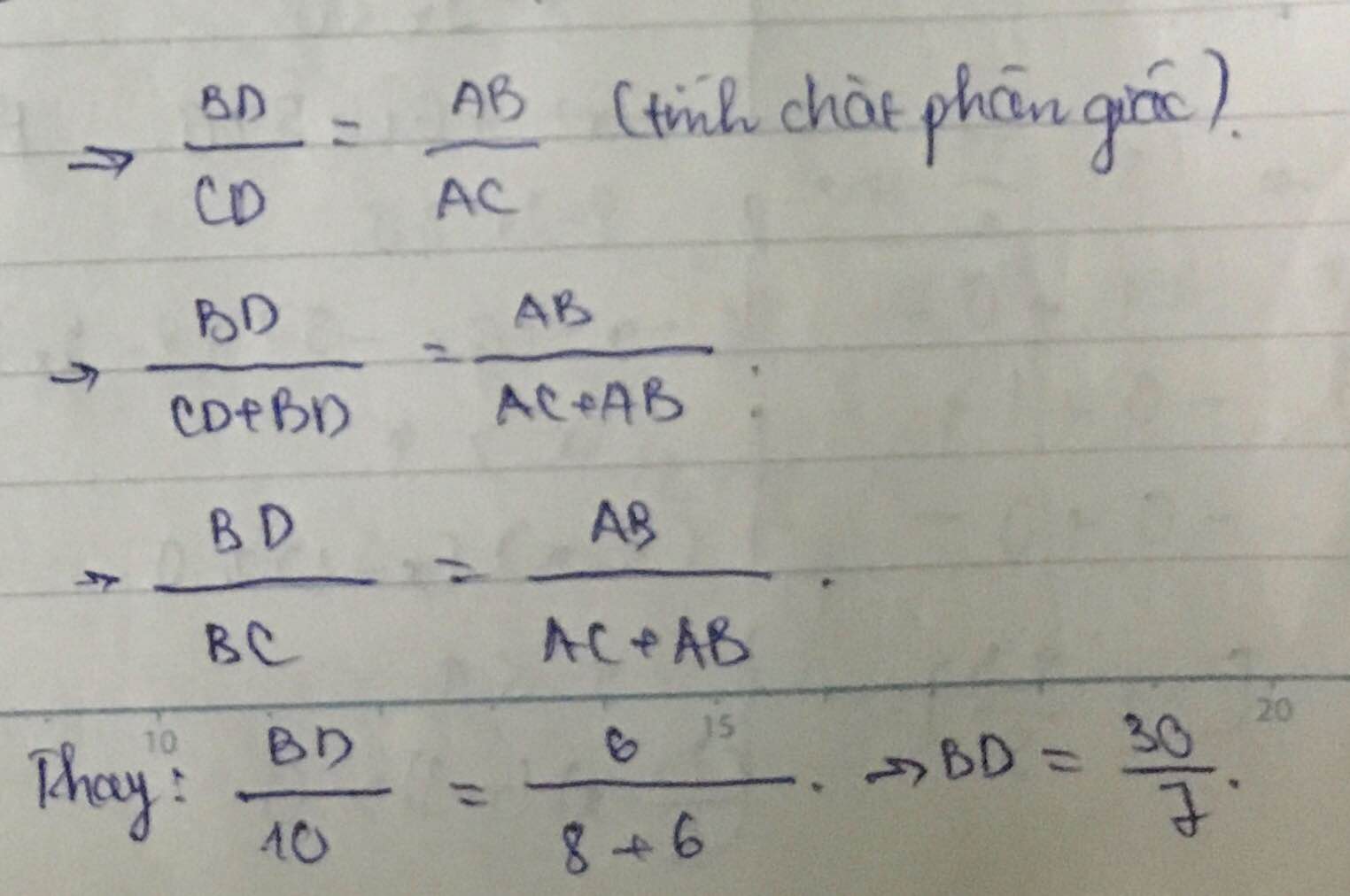
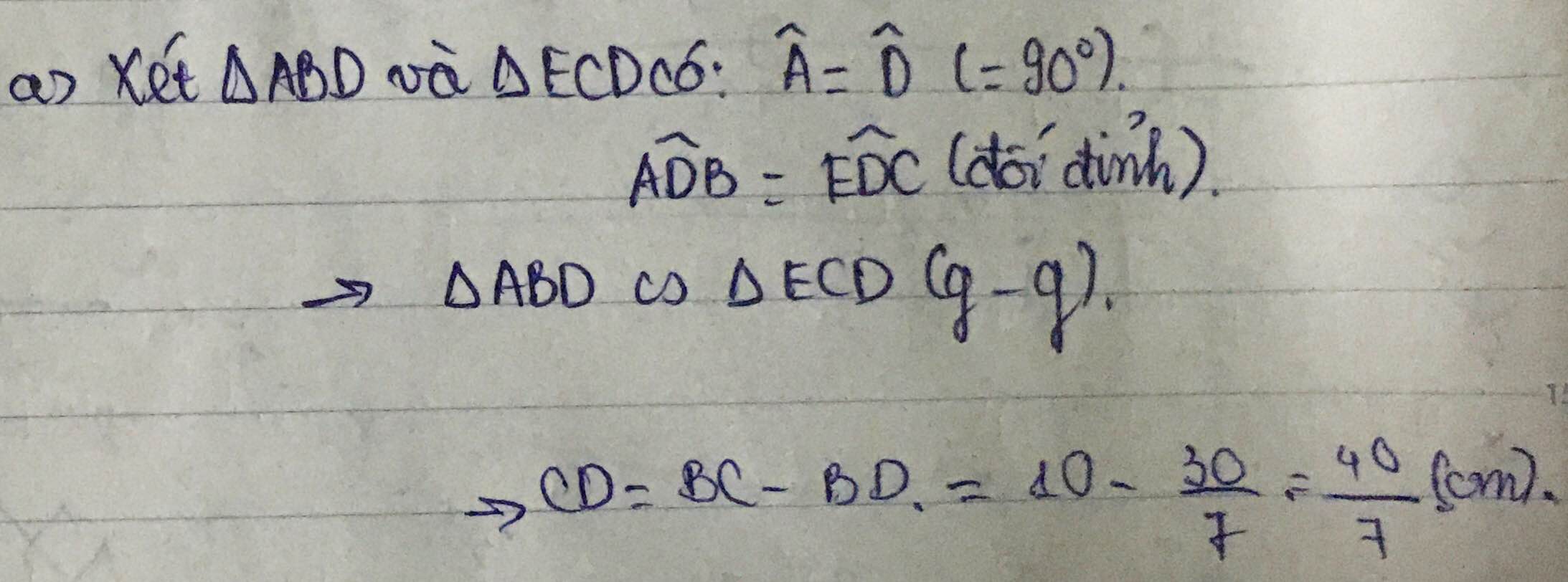
câu a là chứng minh goc BAC nhé