Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do 3 con lắc giống nhau, nên nó cùng vị trí cân bằng. 3 lò xo lại treo cách đều nhau, nên để 3 vật nhỏ gắn ở 3 lò xo luôn thẳng hàng thì con lắc ở giữa có li độ băng trung bình cộng của 2 con lắc kia (bạn có thể vẽ hình ra sẽ thấy rõ hơn)
\(\Rightarrow x_2=\frac{x_1+x_3}{2}\)
Tổng hợp 2 dao động x1 và x3 ta đc: \(x_1+x_3=24\cos\left(\pi t+\frac{5\pi}{12}\right)\)(cm)
\(\Rightarrow x_2=12\cos\left(\pi t+\frac{5\pi}{12}\right)\)

Bài này mình giải ra không được chẵn, có lẽ do giả thiết, mình hướng dẫn cách làm thế này nhé.
+ Cộng 3 biểu thức vế với vế --> x1 + x2 + x3. (vế bên phải là tổng hợp của 3 dao động, dùng máy tính bấm)
+ Tìm biểu thức x1 và x3
+ Biểu diễn bằng véc tơ qua tại thời điểm x1 đang ở biên độ âm, từ đó tìm x2.
vai trò lớn nhất của cư dân phươngđông đối với nhân loại là gì?

Trước tiên ta biểu diễn theo phương trình hình tròn :
Với : \(\varphi=-\frac{\pi}{2}\left(rad\right)=90^O\)
Vật xuất phát từ điểm M (vị trí cân bằng theo chiều dương)
\(\Delta t=t_2-t_1=\frac{\pi}{12}\left(s\right)\)
Góc quét : \(\Delta\varphi=\Delta t.\omega=\frac{\pi}{12}.50=\frac{25\pi}{6}\)
Phân tích góc quét : \(\Delta=\frac{25\pi}{6}=\frac{\left(24+1\right)\pi}{6}=2.2\pi+\frac{\pi}{6}\)
Vậy: \(\Delta\varphi_1=2,2\pi\) ; \(\Delta\varphi_2=\frac{\pi}{6}\)
Khi góc quét \(\Delta\varphi_1=2.2\pi\) thì s1 = 2.4.A =2.4.12 = 96 (quay vòng quanh M)
Khi góc quét : \(\Delta\varphi_2=\frac{\pi}{6}\) vật đi từ M đến N thì s2 = 12cos600
Vậy quãng đường tổng cộng : s1 + s2 = 96 + 6 = 102 (cm)
Biểu diễn dao động điều hòa bằng véc tơ quay, trong thời gian \(\pi/12\)s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega .t =50.\dfrac{\pi}{12}=\dfrac{25\pi}{6}(rad)=4\pi+\dfrac{\pi}{6}\)
+ Véc tơ quay quay đc góc \(4\pi\), bằng 2 chu kì thì quãng đường là: \(S_1=2.4A=8.12=96cm\)
+ Quay thêm góc \(\pi/6\) từ VTCB thì quãng đường đi thêm được là: \(S_2=A/2=6cm\)
Vậy quãng đường vật đi được là: \(S=S_1+S_2=96+6=102cm\)

Chọn B
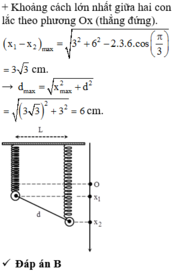
+ Khoảng cách giữa hai vật nhỏ trong quá trình dao động xác định theo công thức:
![]()
+ Đặt: X = x1 – x2 = 3cosωt - 6cos(ωt+π/3) = 3√3 sinωt
+ L có giá trị lớn nhất khi│X│ = Xmax = 3√3
=> Do vậy Lmax = 6cm.

Chọn đáp án A
Vì 3 vật luôn nằm trên một đường thẳng nên ta có:

Bấm máy tính theo số phức như dạng tổng hợp dao động điều hòa ta tính ra được:
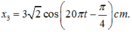

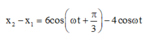
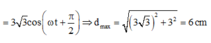
Để 3 vật nhỏ luôn thẳng hàng thì: x2 = (x1 + x3) / 2.
\(\Rightarrow x_2=\frac{24\cos\left(\pi t+\frac{\pi}{2}\right)}{2}=12\cos\left(\pi t+\frac{\pi}{2}\right)\)
Có thể giải thích rõ hơn k? Vì mình cũng đag thắc mắc câu hỏi này. Cám ơn