Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\\ =1-\dfrac{1}{11}=\dfrac{10}{11}\)
\(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+\dfrac{2}{7\cdot9}+\dfrac{2}{9\cdot11}\\ =1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}\\ =1-\dfrac{1}{11}\\ =\dfrac{10}{11}\)

\(\dfrac{3}{4}+\dfrac{2}{5}\times4:\dfrac{8}{3}\)
\(=\dfrac{3}{4}+\dfrac{8}{5}\times\dfrac{3}{8}\)
\(=\dfrac{3}{4}+\dfrac{3}{5}\)
\(=\dfrac{27}{20}\)

Ta có: \(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2020\cdot2021}+\dfrac{1}{2021\cdot2022}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2020}-\dfrac{1}{2021}+\dfrac{1}{2021}-\dfrac{1}{2022}\)
\(=1-\dfrac{1}{2022}=\dfrac{2021}{2022}\)
1/1x2+1/2x3+1/3x4+...+1/2020x2021+1/2021x2022
=1/1-1/2+1/2-1/3+1/3-1/4+...+1/2020-1/2021+1/2021-1/2022.
=1/1-1/2022
=2021/2022

\(=\dfrac{1}{2x1x3x2}+\dfrac{1}{2x2x3x3}+\dfrac{1}{2x3x3x4}+...+\dfrac{1}{2x18x3x19}+\dfrac{1}{2x19x3x20}=\)
\(=\dfrac{1}{2x3}x\left(\dfrac{1}{1x2}+\dfrac{1}{2x3}+\dfrac{1}{3x4}+...+\dfrac{1}{18x19}+\dfrac{1}{19x20}\right)=\)
\(=\dfrac{1}{6}x\left(\dfrac{2-1}{1x2}+\dfrac{3-2}{2x3}+\dfrac{4-3}{3x4}+...+\dfrac{20-19}{19x20}\right)=\)
\(=\dfrac{1}{6}x\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\right)=\)
\(=\dfrac{1}{6}x\left(1-\dfrac{1}{20}\right)=\dfrac{1}{6}x\dfrac{19}{20}=\dfrac{19}{120}\)

\(\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}+\dfrac{1}{9.10}\right).100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\right).100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(1-\dfrac{1}{10}\right).100-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left(100-10\right)-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow90-\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=89\)
\(\Rightarrow\left[\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)\right]:\dfrac{1}{2}=1\)
\(\Rightarrow\dfrac{5}{2}:\left(x+\dfrac{206}{100}\right)=1.2=2\)
\(\Rightarrow\left(x+\dfrac{206}{100}\right)=\dfrac{5}{2}:2=\dfrac{5}{2}.\dfrac{1}{2}=\dfrac{5}{4}\)
\(\Rightarrow x=\dfrac{5}{4}-\dfrac{206}{100}=\dfrac{125}{100}-\dfrac{206}{100}\)
\(\Rightarrow x=-\dfrac{81}{100}\)

Câu 1:
a. $5\frac{1}{10}=5+\frac{1}{10}> 5=\frac{55}{11}> \frac{51}{11}$
Vậy dấu cần điền là >
b.
$\frac{3}{10}=\frac{6}{20}< \frac{6}{11}$

29\(\dfrac{1}{2}\)\(\times\)\(\dfrac{2}{3}\) + 39\(\dfrac{1}{3}\)\(\times\)\(\dfrac{3}{4}\) + \(\dfrac{5}{6}\)
= \(\dfrac{59}{2}\) \(\times\) \(\dfrac{2}{3}\) + \(\dfrac{118}{3}\) \(\times\) \(\dfrac{3}{4}\) + \(\dfrac{5}{6}\)
= \(\dfrac{59}{3}\) + \(\dfrac{59}{2}\) + \(\dfrac{5}{6}\)
= \(\dfrac{295}{6}\) + \(\dfrac{5}{6}\)
= 50

= 59/2 x 2/3+ 118/3 x 3/4 + 5/6
= 59/3+ 59/2+ 5/6
= 118/6+ 177/6+ 5/6
= 50
= 59/2 x 2/3+ 118/3 x 3/4 + 5/6
= 59/3+ 59/2+ 5/6
= 118/6+ 177/6+ 5/6
= 50
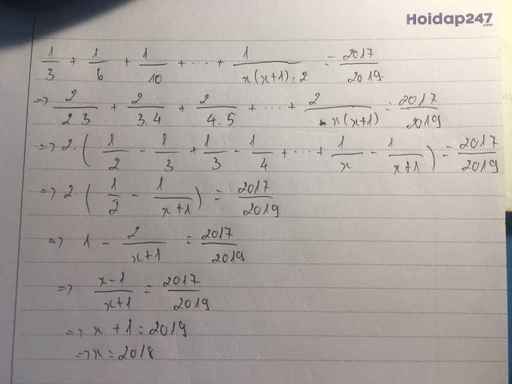
\(A=\dfrac{3}{1.3}+\dfrac{3}{3.5}+\dfrac{3}{5.7}+\dfrac{3}{7.9}+\dfrac{3}{9.11}+\dfrac{3}{11.13}\\ =\dfrac{3}{2}.\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+\dfrac{2}{7.9}+\dfrac{2}{9.11}+\dfrac{2}{11.13}\right)\\ =\dfrac{3}{2}.\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}\right)\\ =\dfrac{3}{2}.\left(1-\dfrac{1}{13}\right)\\ =\dfrac{3}{2}.\dfrac{12}{13}\\ =\dfrac{18}{13}\)
\(A=\dfrac{3}{1.3}+\dfrac{3}{3.5}+\dfrac{3}{5.7}+...+\dfrac{3}{11.13}\\ \dfrac{2A}{3}=\dfrac{2}{1.3}+\dfrac{2}{3.5}+\dfrac{2}{5.7}+...+\dfrac{2}{11.13}\\ \dfrac{2A}{3}=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{11}-\dfrac{1}{13}=1-\dfrac{1}{13}=\dfrac{12}{13}\\ =>A=\dfrac{12}{13}:\dfrac{2}{3}=\dfrac{12}{13}.\dfrac{3}{2}=\dfrac{18}{13}\)