
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có : ab - ba = (a0 + b) - (b0 + a)
= (10 x a + b) - (10 x b + a)
= (10 x a - a) - (10 x b - b)
= 9 x a - 9 x b
= 9 x (a - b) \(⋮\)9
=> (ab - ba) \(⋮\)9 (đpcm)
b) Ta có : ab + ba = a0 + b + b0 + a
= 10 x a + b + b x 10 + a
= (10 x a + a) + (10 x b + b)
= 11 x a + 11 x b
= 11 x (a + b) \(⋮\)11
=> (ab + ba) \(⋮\)11 (đpcm)

c, Ta có ab+ba = 10a + 10b + a + b=11a + 11b
Vậy ab+ba chia hết cho 11

\(\overline{ab}\) + \(\overline{ba}\) = \(a\times\) 10 + \(b\) + \(b\times\) 10 + \(a\) = \(a\times11\) + \(b\times\)11
\(\overline{ab}\) + \(\overline{ba}\) = (\(a\) + \(b\))\(\times\) 11
Vì 11 ⋮ 11 ⇒ (\(a+b\))\(\times\) 11 ⋮ 11 ⇒ \(\overline{ab}\) + \(\overline{ba}\) ⋮ 11 (đpcm)
ab +ba=a x10 +b +b x10 +a=a x[10+1] + b x[10+1]
=a x 11 + b x 11=[a+b] x11
mà : 11chia hết cho 11 nên 11:11=[a+b]
suy ra : a+b có thể là bất kì số gì khác 0

Bởi vì a,b là 2 chữ số khác 0 nên:
ab+ba đặt tính rồi tính ta có
ab Ta có: a+b b+a nên a+b=b+a
+ Ví dụ: cho a=2,b=1
ba Ta có: 21+12=33(chia hết cho 11)
_____

a, abab = ab . 101 chia hết cho 101
b, ab + ba
= 10a +b + 10b +a
= 11a + 11b
= 11(a+b) chia hết cho 11
c, ab-ba
=10a+b - (10b+a)
=9a-9b
=9(a-b) chia hết cho 9

Bạn nhấn vôGiúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
Tích đúng cho mình nha
a, Ta có: abab = ab . 101 chia hết cho 101
b, Ta có: ab + ba = a.10+b + b.10+a = a.11 + b.11 = 11.(a+b) chia hết cho 11 ( dấu . là dấu nhân)
c, Ta có; ab - ba = (a.10+b) - (b.10+a) = a.10+b - b.10-a = 9.a - 9.b = 9.(a-b)
Nhấn đúng cho mk nha!!!!!!!!!!!!

a) ab=a.10+b
ba=b.10+a
ab-ba=10a+b-10b-a
=9a-9.b
Giả sử a lớn hơn b n đơn vị, ta có:
(b+n)9-9b
=n.9 => ab-ba luôn chia hết cho 9
b) ab=10a+b
ba=10b+a
ab+ba=10a+a+10b+b
=11a+11b
=(a+b)11
=> ab+ba luôn chia hết cho 11
chúc bạn học tốt nha
Ta có: ab - ba = 10a + b - (10b + a) = 10a + b - 10b - a = 9a - 9b = 9 x (a - b)
Vì a > b nên a - b dương => 9 x (a - b) chia hết cho 9
ab + ba = 10a + b + 10b + a = 11a + 11b = 11 x (a + b) chia hết cho 11

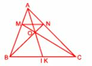
a) Vì AB = 3 x AM, AC = 3 x AN, nên MB = 2/3 x AB, NC = 2/3 x AC.
Từ đó suy ra : dt (MBC) = 2/3 x dt (ABC) (chung chiều cao từ C
dt (NCB) = 2/3 x dt (ABC) (chung chiều cao từ B)
Vậy dt (MBC) = dt (NCB) mà tam giác MBC và tam giác NCB có chung đáy BC, nên chiều cao từ M bằng chiều cao từ N xuống đáy BC hay MN song song với BC. Do đó BMNC là hình thang.
Từ MB = 2/3 x AB, nên dt (MBN) = 2/3 x dt (ABN) (chung chiều cao từ N) hay dt (ABN) = 2/3 x dt (MBN).
Hơn nữa từ AC = 3 x AN, nên NC = 2 x AN, do đó dt (NBC) = 2 x dt (ABN) (chung chiều cao từ B) ; suy ra dt (NBC) = 3/2 x 2 x dt (MBN) = 3 x dt (MBN).
Mà tam giác NBC và tam giác MBN có chiều cao bằng nhau (cùng là chiều cao của hình thang BMNC). Vì vậy đáy BC = 3 x MN.
b) Gọi BN cắt CM tại O. Ta sẽ chứng tỏ AI cũng cắt BN tại O. Muốn vậy, nối AO kéo dài cắt BC tại K, ta sẽ chứng tỏ K là điểm chính giữa của BC (hay K trùng với I).
Theo phần a) ta đã có dt (NBC) = 2 x dt (ABN). Mà tam giác NBC và tam giác ABN có chung đáy BN, nên chiều cao từ C gấp 2 lần chiều cao từ A xuống đáy BN. Nhưng đó là chiều cao tương ứng của hai tam giác BCO và BAO có chung đáy BO, vì vậy dt (BCO) = 2 x dt (BAO)
Tương tự ta cũng có dt (BCO) = 2 x dt (CAO).
Do đó dt (BAO) = dt (CAO). Hai tam giác BAO và CAO có chung đáy AO, nên chiều cao từ B bằng chiều cao từ C xuống đáy AO. Đó cũng là chiều cao tương ứng của hai tam giác BOK và COK có chung đáy OK, vì vậy dt (BOK) = dt (COK). Mà hai tam giác BOK và tam giác COK lại chung chiều cao từ O, nên hai đáy BK = CK hay K là điểm chính giữa của cạnh BC. Vậy điểm K trùng với điểm I hay BN, CM, AI cùng cắt nhau tại điểm O.

Câu b nha:
ab-ba =10a+b+10b+a=11a+11b
=11(a+b)
vì 11 chia hết cho 11 nên 11(a+b) chia hết cho 11
vậy ab+ba chia hết cho11
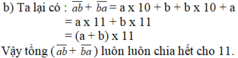
B = 2022 .ab = 337.6.ab vì 337 ⋮ 337 ⇔ 337.6.ab ⋮ 337
⇔ 2022.ab⋮ 337 (đpcm)
\(2022.ab=6.337.ab⋮337\)