
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


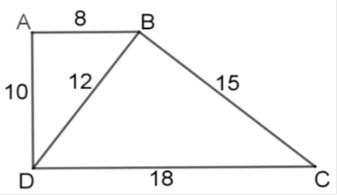
a) Xếp độ dài các cạnh của mỗi tam giác ABD và BDC từ nhỏ đến lớn:8,10,12 và 12,15,18.
Ta có \(\frac{8}{12}=\frac{10}{15}=\frac{12}{18}=\frac{2}{3}\)
=> ΔABC đồng dạng với ΔBDC ( theo c.c.c)
b) ΔABD đồng dạng với ΔBDC
nên \(\widehat{ABD}=\widehat{BDC}\) (So le trong)
=> AB//CD
=> ABCD là hình thang
chúc bạn học tốt:)

Câu 1:
Phân thức đối của phân thức \(\frac{1-x}{x^2+2}\) là \(\frac{x-1}{x^2+2}\)
Câu 2: Tam giác ABC vuông tại A, AB= 12cm, BC=15cm. Trên cạnh BC lấy điểm D sao cho BD=6cm. Kẻ DE⊥AB. Độ dài DE là 3,6 cm.
Câu 3: Thấy hình vẽ đâu bạn.
Chúc bạn học tốt!

Tam giác EAB đồng dạng với tam giác CDE (tam giác vuông, ch-cgv) suy ra góc ABE = góc DEC và góc AEB = góc ECD. Mà ABE + AEB =90 độ nên thay vào ta có DEC + ECD = BEC = 90 độ
Chỉnh sửa: DEC + ECD = 90, mà DEC + ECD + BEC = 180 trừ ra ta có BEC = 90

(bài dễ, nói sơ thôi chắc cũng hiểu, chịu khó nha)
1.
a) trường hợp g.g : có 1 A^ chung với DE//BC => cặp góc đồng vị bằng nhau.
b) kq câu a => tỉ số đồng dạng và các tỉ lệ, thay số đo vào thấy ngay
c) CF//= DE => DF // EC (tứ giác DECF là hbh) => cặp góc đồng vị bằng nhau + B^ chung để cm tgđdạng
2. a) , b) là kết quả điển hình rồi, khỏi nói nhé, còn chưa rõ thì bình luận hay ib gì cũng đc
c) áp dụng đl pytago đảo (từ mấy cái số đo cho ở đầu đề)
d) dùng tính chất đường pg trong tam giác kết hợp tính chất dãy tỉ số bằng nhau đã học ở lớp 7 là ra ngay

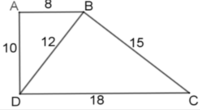
Ta có: A B B D = A D B C = B D D C (vì) 8 12 = 10 15 = 12 18 ( = 2 3 )
Nên ΔABD ~ ΔBDC (c - c - c)
ΔABD ~ ΔBDC nên góc ABD = BDC.
Mà hai góc này ở vị trí so le trong nên AB // CD.
Vậy ABCD là hình thang.
Lại có B D 2 = 144 < 164 = A D 2 + A B 2 nên ΔABD không vuông. Do đó ABCD không là hình thang vuông
Vậy A, B đều đúng, C sai.
Đáp án: D

a: Xét ΔABD và ΔECD có
góc ADB=góc EDC
góc ABD=góc ECD
=>ΔABD đồng dạng với ΔECD
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3=(DB+DC)/(2+3)=15/5=3
=>DB=6cm; DC=9cm