K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
9 tháng 2 2017
a) Xét P(n) : “3n < n + 100”:
+ Với n = 1, P(1) trở thành: “31 < 1 + 100”. Mệnh đề đúng vì 31 = 3 < 1 + 100 = 101.
+ Với n = 2, P(2) trở thành: “32 < 2 + 100”. Mệnh đề đúng vì 32 = 9 < 2 + 100.
+ Với n = 3, P(3) trở thành: “33 < 3 + 100”. Mệnh đề đúng vì 33 = 27 < 3 + 100.
+ Với n = 4, P(4) trở thành: “34 < 4 + 100”. Mệnh đề đúng vì 34 = 81 < 4 + 100.
+ Với n = 5, P(5) trở thành: “35 < 5 + 100”. Mệnh đề sai vì 35 = 243 > 5 + 100.
Xét Q(n): “2n > n”.
+ Với n = 1, Q(1) trở thành: “21 > 1”. Mệnh đề đúng vì 21 = 2 > 1.
+ Với n = 2, Q(2) trở thành: “22 > 2”. Mệnh đề đúng vì 22 = 4 > 2.
+ Với n = 3, Q(3) trở thành: “23 > 3”. Mệnh đề đúng vì 23 = 8 > 3.
+ Với n = 4, Q(4) trở thành: “24 > 4”. Mệnh đề đúng vì 24 = 16 > 4.
+ Với n = 5, Q(5) trở thành: “25 > 5”. Mệnh đề đúng vì 25 = 32 > 5.
b)
+ Nhận thấy P(n) không đúng với mọi n ∈ N* (sai với n = 5).
+ Với mọi n ∈ N*, Q(n) luôn đúng.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
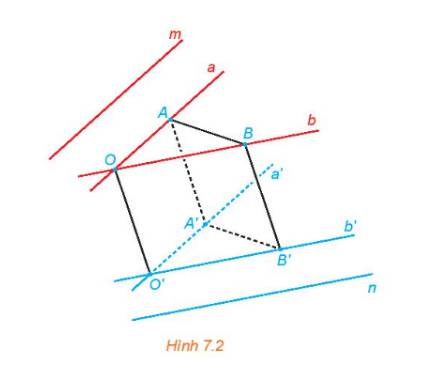
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a', b // b'.
b) Ta có:
+) OA // O′A′; OO' // AA' nên OAA'O' là hình bình hành.
+) OB // O′B′; OO' // BB' nên OBB'O' là hình bình hành.
+) AB // A′B′ và OO' // AA'; OO' // BB' suy ra AA' // BB' nên ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(\cos \left( {a,b} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}};\cos \left( {a',b'} \right) = \frac{{O'{{A'}^2} + O'{{B'}^2} - A'{{B'}^2}}}{{2.O'A'.O'B'}}\)
Vì O'A' = OA và O'B' = OB; AB = A'B' nên cos(a,b) = cos(a′,b′).
16 tháng 8 2023
tham khảo:
a) Vì M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) nên hình chiếu của a trên mặt phẳng (P) là a’ đường thẳng đi qua hai điểm M', N'.
b) b vuông góc với M'N' và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); M'N' cắt MM' tại M' do đó b vuông góc mặt phẳng tạo bởi M'N', MM' suy ra b có vuông góc với a.
c) b vuông góc với a và b vuông góc với MM' (do M' là hình chiếu của M trên (P)); a cắt MM' tại M do đó b vuông góc mặt phẳng tạo bởi a, MM' suy ra b có vuông góc với M'N'.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
Ta có \(MA \bot \left( P \right)\) (A là hình chiếu của M trên (P))
\(NB \bot \left( P \right)\) (B là hình chiếu của N trên (P))
\( \Rightarrow \) MA // NB \( \Rightarrow \) 4 điểm M, A, B, N đồng phẳng
\(\left. \begin{array}{l}\left( {AMNB} \right) \cap \left( P \right) = AB\\a//\left( P \right)\end{array} \right\} \Rightarrow a//AB\)
\( \Rightarrow \) Tứ giác AMNB là hình bình hành.
Mà \(MA \bot AB\left( {MA \bot \left( P \right)} \right)\)
\( \Rightarrow \) Tứ giác AMNB là hình chữ nhật nên MA = NB
Vậy M, N có cùng khoảng cách đến (P).
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 2 2020
Ý bạn là dãy \(5u_n\)
Đặt \(u_n=u_1+\left(n-1\right)d\)
\(v_n=5u_n=5u_1+\left(n-1\right).5d\)
Vậy dãy mới là 1 cấp số cộng với số hạng đầu bằng \(u_1'=5u_1\) và công sai \(d'=5d\)
CM
24 tháng 12 2018
Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.
Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.
SAI