
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét tứ giác DIHK có
góc DIH=góc DKH=góc KDI=90 độ
nên DIHK là hình chữ nhật
b: Xét tứ giác IHAK có
IH//AK
IH=AK
Do đó: IHAK là hình bình hành
=>B là trung điểm chung của IA và HK
Xét ΔIKA có IC/IK=IB/IA
nên BC//KA
Xét ΔIDA có IB/IA=IM/ID
nên BM//DA
=>B,C,M thẳng hàng

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

Ta có: DE//AC (cùng vuông góc với AB)
Áp dụng định lý Ta-lét ta có:
\(\dfrac{BD}{AD}=\dfrac{BE}{CE}\Rightarrow\dfrac{BD}{AD}=\dfrac{BE}{BC-BE}\Rightarrow\dfrac{6}{x}=\dfrac{3x}{13,5-3x}\)
\(\Leftrightarrow6\left(13,5-3x\right)=x\cdot3x\)
\(\Leftrightarrow81-18x=3x^2\)
\(\Leftrightarrow27-6x=x^2\)
\(\Leftrightarrow x^2+6x-27=0\)
\(\Leftrightarrow x^2-3x+9x-27=0\)
\(\Leftrightarrow x\left(x-3\right)+9\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-9\left(ktm\right)\end{matrix}\right.\)
Vậy: `x=3`

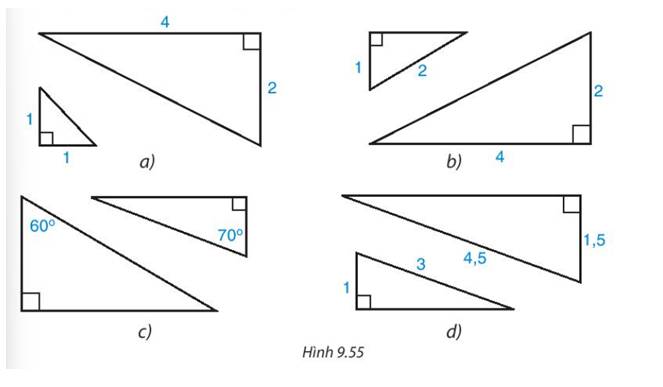
Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.

Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

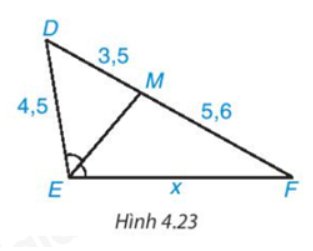
Trong Hình 4.23 có \(\widehat {DME} = \widehat {MEF}\) nên EM là tia phân giác của \(\widehat {{\rm{DEF}}}\).
Áp dụng tính chất đường phân giác của tam giác, ta có:
\(\dfrac{{E{\rm{D}}}}{{EF}} = \dfrac{{M{\rm{D}}}}{{MF}}\) hay \(\dfrac{{4,5}}{x} = \dfrac{{3,5}}{{5,6}}\)
Suy ra: \(x = \dfrac{{5,6.4,5}}{{3,5}} = 7,2\)(đvđd)
Vậy x = 7,2 (đvđd).

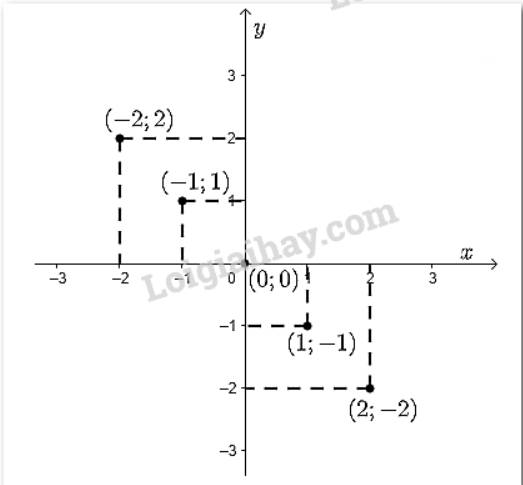
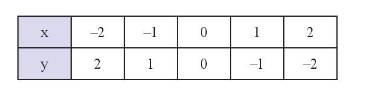
Đồ thị hàm số là tập hợp các điểm có tọa độ \(\left( { - 2;2} \right);\left( { - 1;1} \right);\left( {0;0} \right);\left( {1; - 1} \right);\left( {2; - 2} \right)\) được vẽ trên mặt phẳng tọa độ như hình dưới đây:









2A:
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
AH vuông góc BD
CK vuông góc BD
=>AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
=>AHCK là hình bình hành
làm hết đc ko bạn