
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1,\(\sqrt{\left(x-1\right)^2}=\left|x-1\right|=-\left(x-1\right)=1-x\)
2,\(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=-\left(a-2b\right)=2b-a\)
3,\(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)

Bài 2:
a: Ta có: \(\sqrt{2x-4}=2\)
\(\Leftrightarrow2x-4=4\)
hay x=4
b: Ta có: \(\sqrt{5x}=5\)
nên 5x=25
hay x=5
c: Ta có: \(\sqrt{2x^2+1}=x-1\)
\(\Leftrightarrow2x^2+1=x^2-2x+1\)
hay x=0(loại)

\(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{6^2}{10}=3.6\left(cm\right)\\y=10-3.6=6.4\left(cm\right)\end{matrix}\right.\)


câu a ) đường thẳng đi qua điểm A) thay x=3 , y= -4 , vào pt rồi tìm đenta, điểm B thì x=-4 , y=3 tìm đenta
câu b) chứng minh pt có 2 nghiệm phân biệt đenta >= 0
theo định lý vi ét x1+x2=
x1.x2=
theo đề bài ta có thay vô

2:
a: =>x^2(5x^2+2)+2=0
x^2>=0
5x^2+2>=2
=>x^2(5x^2+2)>=0 với mọi x
=>x^2(5x^2+2)+2>=2>0 với mọi x
=>PTVN
b: x^4-12x^2+24=0
=>x^4-12x^2+36-12=0
=>(x^2-6)^2-12=0
=>(x^2-6-2căn 3)(x^2-6+2căn 3)=0
=>x^2=6+2căn 3 hoặc x^2=6-2căn 3
=>\(x=\pm\sqrt{6+2\sqrt{3}};x=\pm\sqrt{6-2\sqrt{3}}\)

Đề thế này đúng không
(x2 - 8)2 + 36 = x4 - 16x2 + 100
= (x4 + 20x2 + 100) - 36x2
= (x2 + 10)2 - 36x2 = (x2 + 10 + 6x)(x2 + 10 - 6x)

a: Thay \(x=7-4\sqrt{3}\) vào A, ta được:
\(A=2-\sqrt{3}-7+4\sqrt{3}=3\sqrt{3}-5\)

a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)



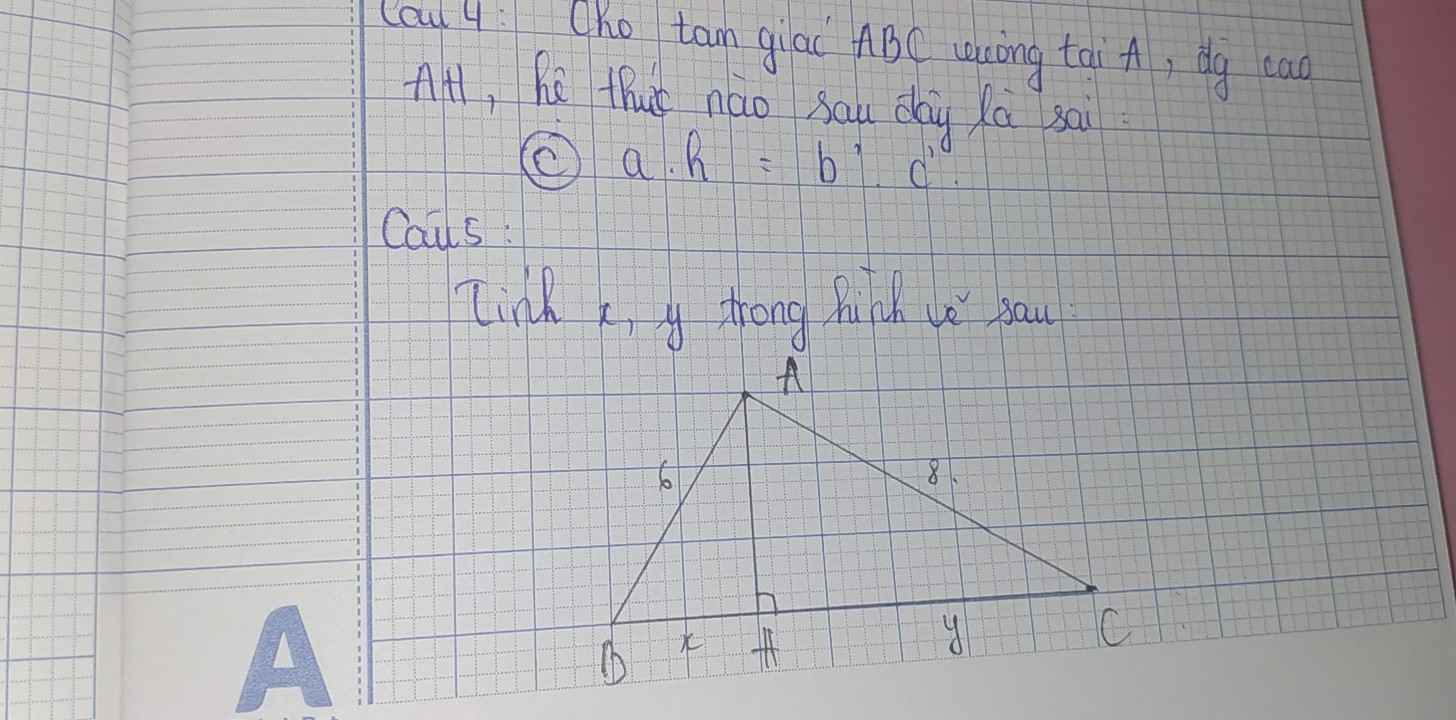

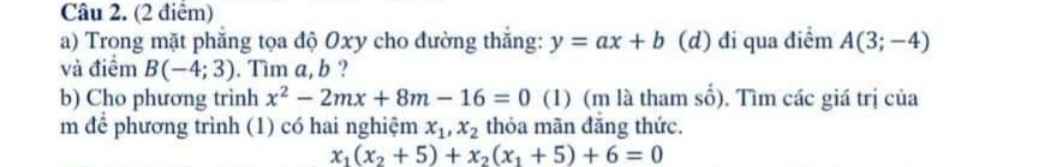
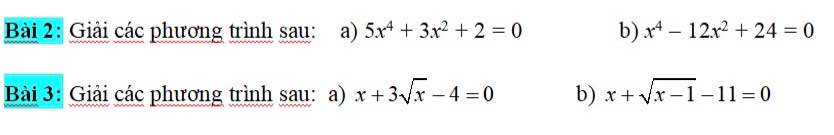

ĐK: \(x,y\ne0\).
Đặt \(\frac{1}{x}=a,\frac{1}{y}=b\).
Hệ phương trình trở thành:
\(\hept{\begin{cases}9a+4b=\frac{23}{10}\\3a+b=\frac{7}{10}\end{cases}}\Leftrightarrow\hept{\begin{cases}9a+4b=\frac{23}{10}\\9a+3b=\frac{21}{10}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{1}{5}\\a=\frac{1}{6}\end{cases}}\Rightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{6}\\\frac{1}{y}=\frac{1}{5}\end{cases}}\)
Suy ra \(\hept{\begin{cases}x=6\\y=5\end{cases}}\)(thỏa mãn)