K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 11 2021
a: Hàm số nghịch biến trên R
b: \(\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\dfrac{x_1^2-4x_1+5-x_2^2+4x_2-5}{x_1-x_2}\)
\(=x_1+x_2-4\)
Trường hợp 1: x<=2
\(\Leftrightarrow x_1+x_2-4< =0\)
Vậy: Hàm số nghịch biến khi x<=2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2021
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x+1\ge0\\x^2-3x+2\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ne\left\{1;2\right\}\end{matrix}\right.\)
Hay \(D=[-1;1)\cup\left(1;2\right)\cup\left(2;+\infty\right)\)
b. \(\left\{{}\begin{matrix}x+2\ge0\\1-x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge-2\\x\ne1\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}1+x\ge0\\1-x\ge0\end{matrix}\right.\) \(\Leftrightarrow-1\le x\le1\)
d. \(\left\{{}\begin{matrix}1-4x^2\ge0\\x^2-2x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}\le x\le\dfrac{1}{2}\\x\ne0\end{matrix}\right.\)
23 tháng 9 2021
\(A=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-5\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2022
\(\dfrac{2x+3}{x-1}\ge1\Leftrightarrow\dfrac{2x+3}{x-1}-1\ge0\)
\(\Leftrightarrow\dfrac{x+4}{x-1}\ge0\)
\(\Rightarrow\left[{}\begin{matrix}x\le-4\\x>1\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
1 tháng 12 2021
Tham khảo tại link sau:
https://hoc24.vn/cau-hoi/ai-giup-em-cau-2-voi-a.3401576227354
19 tháng 12 2021
\(\Leftrightarrow\left\{{}\begin{matrix}3x_1+x_2=-2\\x_1+x_2=2m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=-2m\\x_1+x_2=2m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-m\\x_2=2m-2+m=3m-2\end{matrix}\right.\)
\(x_1\cdot x_2=m^2-3m\)
\(\Leftrightarrow-3m^2+2m-m^2+3m=0\)
\(\Leftrightarrow-4m^2+5m=0\)
\(\Leftrightarrow m\left(4m-5\right)=0\)
=>m=0 hoặc m=5/4
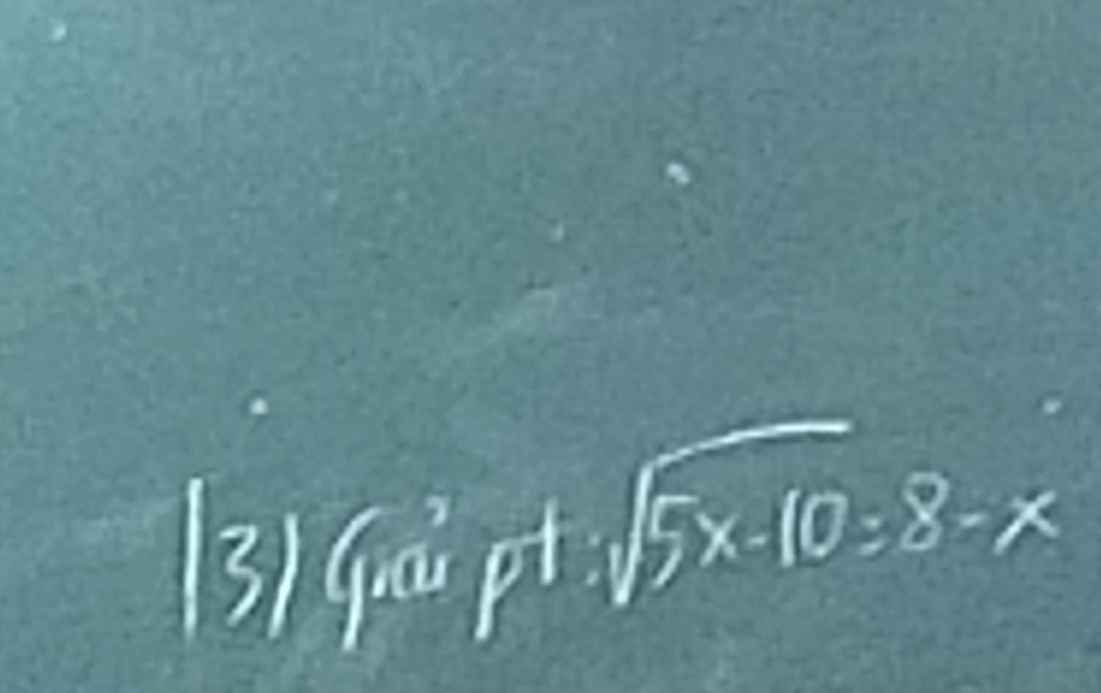
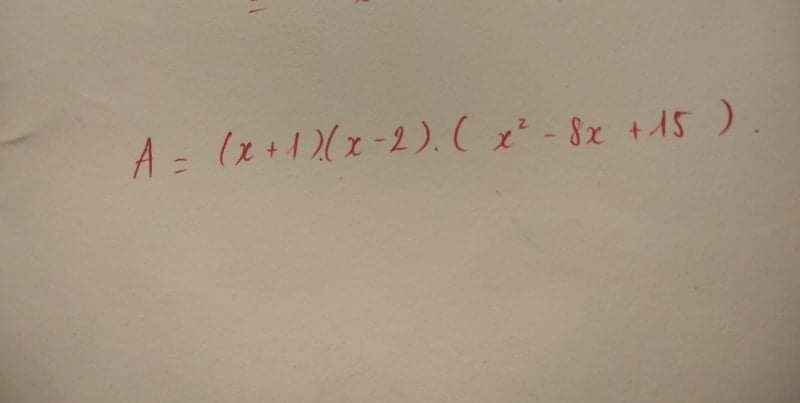
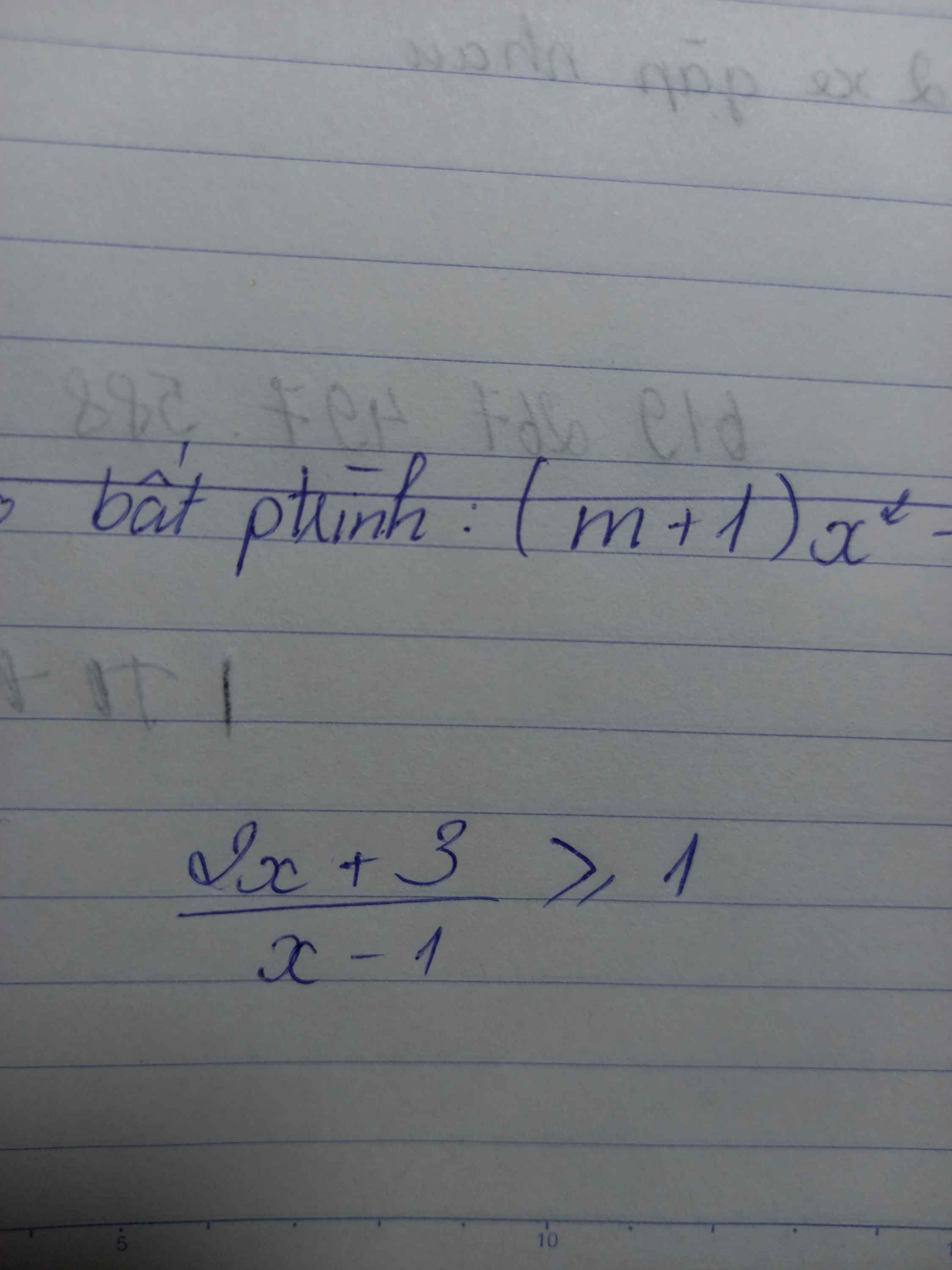
Điều kiện: \(\left\{{}\begin{matrix}5x-10\ge0\\8-x\ge0\end{matrix}\right.\)\(\Leftrightarrow2\le x\le8\)
Bình phương hai vế ta được: \(5x-10=\left(8-x\right)^2\)
\(\Leftrightarrow5x-10=64-16x+x^2\)
\(\Leftrightarrow x^2-21x+74=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{21+\sqrt{145}}{2}\left(loai\right)\\x=\dfrac{21-\sqrt{145}}{2}\left(nhan\right)\end{matrix}\right.\)
Vậy nghiệm của phương trình là \(x=\dfrac{21-\sqrt{145}}{2}\)