Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\dfrac{19}{33}=\dfrac{38}{66};\dfrac{6}{12}=\dfrac{1}{2}=\dfrac{33}{66};\dfrac{13}{22}=\dfrac{39}{66}\)
Mà \(\dfrac{33}{66}< \dfrac{38}{66}< \dfrac{39}{66}\Rightarrow\dfrac{6}{12}< \dfrac{19}{33}< \dfrac{13}{22}\)
Vậy các số hữu tỉ được sắp xếp theo thứ tự tăng dần là: \(\dfrac{6}{12};\dfrac{19}{33};\dfrac{13}{22}\)
b) Ta có:
\(\dfrac{-18}{12}=\dfrac{-3}{2}=\dfrac{-105}{70};\dfrac{-10}{7}=\dfrac{-100}{70};\dfrac{-8}{5}=\dfrac{-112}{70}\)
Mà \(\dfrac{-112}{70}< \dfrac{-105}{70}< \dfrac{-100}{70}\Rightarrow\dfrac{-8}{5}< \dfrac{-18}{12}< \dfrac{-10}{7}\)
Vậy các số hữu tỉ được sắp xếp theo thứ tự tăng dần là: \(\dfrac{-8}{5};\dfrac{-18}{12};\dfrac{-10}{7}\)
a. \(\dfrac{19}{33};\dfrac{6}{12};\dfrac{13}{22}\) ( \(MC=132\) )
Quy đồng : \(\dfrac{19}{33}=\dfrac{76}{132}\) ; \(\dfrac{6}{12}=\dfrac{66}{132}\) ; \(\dfrac{13}{22}=\dfrac{78}{132}\)
Vì \(\dfrac{66}{132}< \dfrac{76}{132}< \dfrac{78}{132}\) => \(\dfrac{6}{12}< \dfrac{19}{33}< \dfrac{13}{22}\)
b. \(\dfrac{-18}{12};\dfrac{-10}{7};\dfrac{-8}{5}\) ( \(MC=420\) )
Quy đồng : \(\dfrac{-18}{12}=\dfrac{-630}{420}\) ; \(\dfrac{-10}{7}=\dfrac{-600}{420}\) ; \(\dfrac{-8}{5}=\dfrac{-672}{420}\)
Vì : \(\dfrac{-672}{420}< \dfrac{-630}{420}< \dfrac{-600}{420}\) => \(\dfrac{-8}{5}< \dfrac{-18}{12}< \dfrac{-10}{7}\)

a: \(\dfrac{-5}{6}=\dfrac{-20}{24};\dfrac{7}{8}=\dfrac{21}{24};\dfrac{7}{24}=\dfrac{7}{24};\dfrac{-3}{4}=-\dfrac{18}{24};\dfrac{2}{3}=\dfrac{16}{24}\)
Do đó: \(\dfrac{-5}{6}< -\dfrac{3}{4}< \dfrac{7}{24}< \dfrac{2}{3}< \dfrac{7}{8}\)
\(\dfrac{7}{8}=\dfrac{119}{136};\dfrac{16}{17}=\dfrac{128}{136}\)
mà 119<128
nên 7/8<16/17
DO đó: -5/6<-3/4<7/24<2/3<7/8<16/17
b: \(\dfrac{-5}{8}=\dfrac{-95}{8\cdot19};\dfrac{-16}{19}=\dfrac{-128}{19\cdot8}\)
Do đó: -5/8>-16/19
\(\dfrac{7}{10}=0.7;\dfrac{20}{23}\simeq0.87;\dfrac{214}{315}\simeq0.68;\dfrac{205}{107}>1\)
Do đó: \(\dfrac{205}{107}>\dfrac{20}{23}>\dfrac{7}{10}>\dfrac{214}{315}>-\dfrac{5}{8}>-\dfrac{16}{19}\)

Giải:
a)
\(\dfrac{7}{48}=\dfrac{105}{720};\)
\(\dfrac{11}{72}=\dfrac{110}{720};\)
\(\dfrac{17}{120}=\dfrac{102}{720}\)
Vì \(102< 105< 110\)
\(\Leftrightarrow\dfrac{102}{720}< \dfrac{105}{720}< \dfrac{110}{720}\)
\(\Leftrightarrow\dfrac{17}{120}< \dfrac{7}{48}< \dfrac{11}{72}\)
Vậy ...
b) \(\dfrac{31}{49}=\dfrac{60140}{95060};\)
\(\dfrac{62}{97}=\dfrac{60760}{95060};\)
\(\dfrac{93}{140}=\dfrac{63147}{95060}\)
Vì \(60140< 60760< 63147\)
\(\Leftrightarrow\dfrac{60140}{95060}< \dfrac{60760}{95060}< \dfrac{63147}{95060}\)
\(\Leftrightarrow\dfrac{31}{49}< \dfrac{62}{97}< \dfrac{93}{140}\)
Vậy ...
a ) \(\dfrac{7}{48}\) = \(\dfrac{105}{720}\)
\(\dfrac{11}{72}\) = \(\dfrac{110}{720}\)
\(\dfrac{17}{120}\) = \(\dfrac{102}{720}\)
Vì 102 < 105 < 110
\(\Leftrightarrow\) \(\dfrac{102}{720}\) < \(\dfrac{105}{720}\) < \(\dfrac{110}{720}\)
\(\Leftrightarrow\) \(\dfrac{17}{120}\) < \(\dfrac{7}{48}\) < \(\dfrac{11}{72}\)
Vậy .....................
( k cho tớ nha . Tớ chỉ bt lm phần a )

Bài 1:
a) \(\left(\dfrac{3}{8}+\dfrac{-3}{4}+\dfrac{7}{12}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\left(\dfrac{9}{24}+\dfrac{-18}{24}+\dfrac{14}{24}\right):\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}:\dfrac{5}{6}+\dfrac{1}{2}\)
\(=\dfrac{5}{24}.\dfrac{6}{5}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{1}{2}\)
\(=\dfrac{1}{4}+\dfrac{2}{4}\)
\(=\dfrac{3}{4}\)
b) \(\dfrac{1}{2}+\dfrac{3}{4}-\left(\dfrac{3}{4}-\dfrac{4}{5}\right)\)
\(=\dfrac{1}{2}+\dfrac{3}{4}-\dfrac{3}{4}+\dfrac{4}{5}\)
\(=\left(\dfrac{1}{2}+\dfrac{4}{5}\right)+\left(\dfrac{3}{4}-\dfrac{3}{4}\right)\)
\(=\dfrac{1}{2}+\dfrac{4}{5}\)
\(=\dfrac{5}{10}+\dfrac{8}{10}\)
\(=\dfrac{9}{5}\)
c) \(6\dfrac{5}{12}:2\dfrac{3}{4}+11\dfrac{1}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}:\dfrac{11}{4}+\dfrac{42}{4}.\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{77}{12}.\dfrac{4}{11}+\dfrac{42}{4}.\left(\dfrac{5}{15}+\dfrac{3}{15}\right)\)
\(=\dfrac{7}{3}+\dfrac{42}{4}.\dfrac{8}{15}\)
\(=\dfrac{7}{3}+\dfrac{14.2}{1.3}\)
\(=\dfrac{7}{3}+\dfrac{28}{3}\)
\(=\dfrac{35}{3}\)
d) \(\left(\dfrac{7}{8}-\dfrac{3}{4}\right).1\dfrac{1}{3}-\dfrac{2}{7}.\left(3,5\right)^2\)
\(=\left(\dfrac{7}{8}-\dfrac{6}{8}\right).\dfrac{4}{3}-\dfrac{2}{7}.12\dfrac{1}{4}\)
\(=\dfrac{1}{8}.\dfrac{4}{3}-\dfrac{2}{7}.\dfrac{49}{4}\)
\(=\dfrac{1}{6}-\dfrac{7}{2}\)
\(=\dfrac{1}{6}-\dfrac{21}{6}\)
\(=\dfrac{-10}{3}\)
e) \(\left(\dfrac{3}{5}+0,415-\dfrac{3}{200}\right).2\dfrac{2}{3}.0,25\)
\(=\left(\dfrac{3}{5}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\left(\dfrac{120}{200}+\dfrac{83}{200}-\dfrac{3}{200}\right).\dfrac{8}{3}.\dfrac{1}{4}\)
\(=1.\dfrac{8}{3}.\dfrac{1}{4}\)
\(=\dfrac{2}{3}\)
f) \(\dfrac{5}{16}:0,125-\left(2\dfrac{1}{4}-0,6\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}:\dfrac{1}{8}-\left(\dfrac{9}{4}-\dfrac{3}{5}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{16}.\dfrac{8}{1}-\left(\dfrac{45}{20}-\dfrac{12}{20}\right).\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{33}{20}.\dfrac{10}{11}\)
\(=\dfrac{5}{2}-\dfrac{3}{2}\)
\(=\dfrac{2}{2}=1\)
g) \(0,25:\left(10,3-9,8\right)-\dfrac{3}{4}\)
\(=\dfrac{1}{4}:\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{1}{4}.\dfrac{2}{1}-\dfrac{3}{4}\)
\(=\dfrac{1}{2}-\dfrac{3}{4}\)
\(=\dfrac{2}{4}-\dfrac{3}{4}\)
\(=\dfrac{-1}{4}\)
h) \(1\dfrac{13}{15}.0,75-\left(\dfrac{11}{20}+20\%\right):\dfrac{7}{3}\)
\(=\dfrac{28}{15}.\dfrac{3}{4}-\left(\dfrac{11}{20}+\dfrac{1}{5}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\left(\dfrac{11}{20}+\dfrac{4}{20}\right):\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{3}{4}:\dfrac{7}{3}\)
\(=\dfrac{7}{5}-\dfrac{9}{28}\)
\(=\dfrac{196}{140}-\dfrac{45}{140}\)
\(=\dfrac{151}{140}\)
i) \(\dfrac{\left(\dfrac{1}{2-0,75}\right).\left(0,2-\dfrac{2}{5}\right)}{\dfrac{5}{9}-1\dfrac{1}{12}}\)
\(=\dfrac{\left(\dfrac{1}{1,25}\right).\left(\dfrac{1}{5}-\dfrac{2}{5}\right)}{\dfrac{5}{9}-\dfrac{13}{12}}\)
\(=\dfrac{\dfrac{1}{1,25}.\dfrac{-1}{5}}{\dfrac{20}{36}-\dfrac{39}{36}}\)
\(=\dfrac{\dfrac{-1}{6,25}}{\dfrac{-19}{36}}\)
k) \(\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{1}{14}}{-1-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{2}{28}}{-\dfrac{3}{3}-\dfrac{3}{7}+\dfrac{3}{28}}\)
\(=\dfrac{2\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}{\left(-3\right)\left(\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{28}\right)}\)
\(=-\dfrac{2}{3}\)
\(A=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(A=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{3}{8}.\dfrac{5}{28}\)
\(A=\left(\dfrac{7}{10}.\dfrac{5}{28}\right).\left(\dfrac{8}{3}.\dfrac{3}{8}\right).20\)
\(A=\dfrac{1}{8}.1.20\)
\(A=\dfrac{20}{8}=\dfrac{5}{2}\)
\(B=\left(9\dfrac{30303}{80808}+7\dfrac{303030}{484848}\right)+4,03\)
\(B=\left(9\dfrac{3}{8}+7\dfrac{5}{8}\right)+4,03\)
\(B=\left[\left(9+7\right)+\left(\dfrac{3}{8}+\dfrac{5}{8}\right)\right]+4,03\)
\(B=\left(16+1\right)+4,03\)
\(B=17+4,03\)
\(B=21,03\)
\(C=\left(9,75.21\dfrac{3}{7}+\dfrac{39}{4}.18\dfrac{4}{7}\right).\dfrac{15}{78}\)
\(C=\left(\dfrac{39}{4}.\dfrac{150}{7}+\dfrac{39}{4}.\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.\left(\dfrac{150}{7}+\dfrac{130}{7}\right).\dfrac{15}{78}\)
\(C=\dfrac{39}{4}.40.\dfrac{15}{78}\)
\(C=390.\dfrac{15}{78}\)
\(C=75\)

1) \(\dfrac{3}{2}\) : \(\dfrac{9}{4}\) =\(\dfrac{3}{2}\)x\(\dfrac{4}{9}\)=\(\dfrac{12}{18}\)=\(\dfrac{2}{3}\)
2)\(\dfrac{48}{55}\) : \(\dfrac{12}{11}\)= \(\dfrac{48}{55}\) x\(\dfrac{11}{12}\)= \(\)\(\dfrac{528}{660}\)=\(\dfrac{4}{5}\)
3)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\)=\(\dfrac{7}{10}\) x \(\dfrac{5}{7}\)= \(\dfrac{35}{70}\)=\(\dfrac{1}{2}\)
4)\(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) = \(\dfrac{6}{7}\) x \(\dfrac{7}{8}\) =\(\dfrac{42}{56}\)=\(\dfrac{3}{4}\)
Sắp xếp các thương theo thứ tự tăng dần :\(\dfrac{1}{2}\);\(\dfrac{2}{3}\);\(\dfrac{3}{4}\);\(\dfrac{4}{5}\)
\(\Rightarrow\)\(\dfrac{7}{10}\) : \(\dfrac{7}{5}\) ; \(\dfrac{3}{2}\) :\(\dfrac{9}{4}\) ; \(\dfrac{6}{7}\) : \(\dfrac{8}{7}\) ; \(\dfrac{48}{55}\):\(\dfrac{12}{11}\).

1)
a)
\(\dfrac{-21}{28}=\dfrac{\left(-21\right):7}{28:7}=\dfrac{-3}{4}\\ \dfrac{-39}{52}=\dfrac{\left(-39\right):13}{52:13}=\dfrac{-3}{4}\)
Vì \(\dfrac{-3}{4}=\dfrac{-3}{4}\) nên \(\dfrac{-21}{28}=\dfrac{-39}{52}\)
b)
\(\dfrac{-1717}{2323}=\dfrac{\left(-17\right)\cdot101}{23\cdot101}=\dfrac{-17}{23}\\ \dfrac{-171717}{232323}=\dfrac{\left(-17\right)\cdot10101}{23\cdot10101}=\dfrac{-17}{23}\)
Vì \(\dfrac{-17}{23}=\dfrac{-17}{23}\) nên \(\dfrac{-1717}{2323}=\dfrac{-171717}{232323}\)
2)
Theo tính chất cơ bản của phân số ta có: \(\dfrac{a}{b}=\dfrac{a\cdot m}{b\cdot m}\) mà \(m\ne n\)
nên không thể.
Trường hợp duy nhất là khi \(a=0\)
Khi đó: \(\dfrac{a}{b}=\dfrac{0}{b}=\dfrac{0\cdot m}{b\cdot n}=\dfrac{0}{b\cdot n}=0\)
3)
Gọi ƯCLN\(\left(12n+1,30n+2\right)\) là \(d\)
Ta có:
\(12n+1⋮d\\ \Rightarrow5\cdot\left(12n+1\right)⋮d\left(1\right)\\ \Leftrightarrow60n+5⋮d\\ 30n+2⋮d\\ \Rightarrow2\cdot\left(30n+2\right)⋮d\\ \Leftrightarrow60n+4⋮d\left(2\right)\)
Từ (1) và (2) ta có:
\(\left(60n+5\right)-\left(60n+4\right)⋮d\\ \Leftrightarrow1⋮d\\ \Rightarrow d=1\)
Vậy ƯCLN\(\left(12n+1,30n+2\right)=1\)
Mà hai số có ƯCLN = 1 thì hai số đó nguyên tố cùng nhau và không có ước chung nào khác
\(\Rightarrow\dfrac{12n+1}{30n+2}\)tối giản

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)
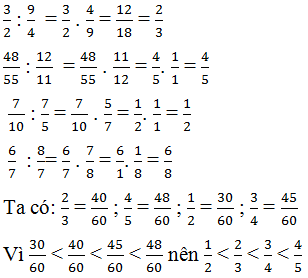
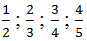


a; Vì : \(\dfrac{-8}{21}\) = \(\dfrac{-16}{42}\) < \(\dfrac{-15}{42}\) = \(\dfrac{-5}{14}\) < \(\dfrac{7}{18}\)=\(\dfrac{14}{36}\) < \(\dfrac{15}{36}\) = \(\dfrac{5}{12}\)
Vậy các phân số đã cho được sắp xếp theo thứ tự tăng dần là:
- \(\dfrac{8}{21}\); - \(\dfrac{5}{14}\); \(\dfrac{7}{18}\); \(\dfrac{5}{12}\)
b; Vì: \(\dfrac{49}{280}\) = \(\dfrac{7}{40}\)= \(\dfrac{14}{80}\) > \(\dfrac{14}{82}\) = \(\dfrac{7}{41}\) = \(\dfrac{14}{82}\) > \(\dfrac{14}{84}\) = \(\dfrac{1}{6}\) = \(\dfrac{21}{126}\) = \(\dfrac{14}{84}\) > \(\dfrac{14}{105}\)
Vậy các phân số đã cho được sắp xếp theo thứ tự tăng dần là:
\(\dfrac{14}{105}\); \(\dfrac{21}{126}\); \(\dfrac{7}{41}\); \(\dfrac{49}{280}\)