Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

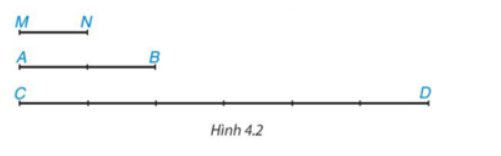
Dùng thước thẳng, dễ dàng đo được đoạn MN dài 1,5cm
\(\Rightarrow\left\{{}\begin{matrix}AB=2\cdot MN=2\cdot1,5=3\left(cm\right)\\CD=6\cdot MN=6\cdot1,5=9\left(cm\right)\end{matrix}\right.\)
Vậy \(\dfrac{AB}{CD}=\dfrac{3}{9}=\dfrac{1}{3}.\)

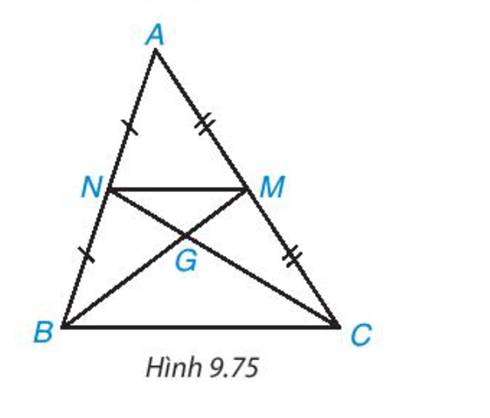
- Xét tam giác ABC có, NA=NB, MA=MC
=> NM là đường trung bình của tam giác ABC
=> NM // BC, \(NM = \frac{1}{2}AB\)
- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC

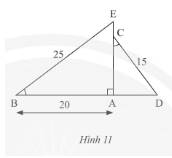
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)

- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)

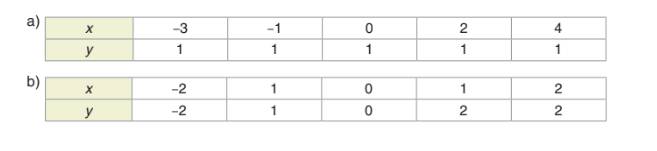
a) Đại lượng y là hàm số của x vì với mỗi giá trị của x (thuộc tập hợp {-3; -1; 0; 2; 4}) ta luôn xác định được chỉ một giá trị tương ứng của y (y luôn bằng 1).
b) Đại lượng y không là hàm số của x vì với x = 1 ta xác định được hai giá trị tương ứng của y là y = 1 và y = 2.

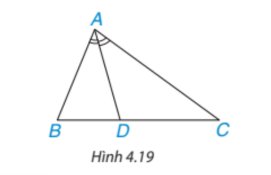
Dựa vào tính chất đường phân giác trong tam giác với tam giác ABC có AD là phân giác của góc \(\widehat{BAC}\) , ta được: \(\dfrac{DB}{DC}=\dfrac{AB}{AC}\).

Chọn đoạn MN làm đơn vị độ dài thì MN = 1 (đvđd).
Khi đó, AB = 2 (đvđd); CD = 6 (đvđd).
Do đó \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{2}{6} = \dfrac{1}{3}\)
Vậy AB = 2 (đvđd); CD = 6 (đvđd); \(\dfrac{{AB}}{{C{\rm{D}}}} = \dfrac{1}{3}\)

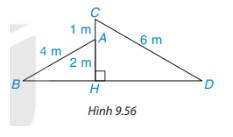
Xét hai tam giác vuông HBA và tam giác vuông HDC nhận thấy:
\(\frac{{AB}}{{C{\rm{D}}}} = \frac{{AH}}{{CH}} = \frac{2}{3}\)
=> Hai tam giác đồng dạng
\( \Rightarrow \widehat {AB{\rm{D}}} = \widehat {C{\rm{D}}B}\)



a) Tỉ số giữa hai số 5 và 8 là \(5:8 = \frac{5}{8}\).
b) Tỉ số giữa hai đoạn thẳng \(AB\) và \(CD\) là \(AB:CD=\dfrac{AB}{CD}=\dfrac{3}{4}\)