K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TP
2
17 tháng 9 2021
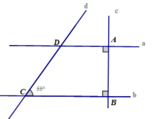
a) Ta có: \(a\perp AB\)
\(b\perp AB\)
=> a//b( từ vuông góc đến song song)
b) Ta có: a//b(cmt)
\(\Rightarrow\widehat{C}=180^0-\widehat{D}=180^0-120^0=60^0\)(2 góc trong cung phía)
5 tháng 7 2021
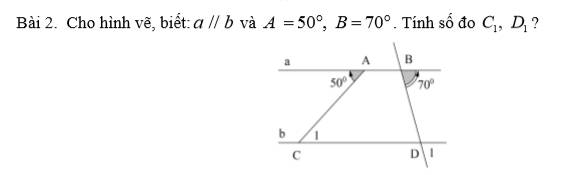
a, - Thấy : \(\widehat{A}+\widehat{B}=180^o\)
Mà 2 góc A và B ở vị trí trong cùng phía .
=> a // b .
b, Ta có : \(\widehat{D}+\widehat{C}=180^o\) ( a//b )
Mà \(\widehat{D}=120^o\)
\(\Rightarrow\widehat{C}=180-120=60^o\)
Vậy ...
12 tháng 11 2021
a, Vì a//b và b⊥c nên a⊥c
b, Ta có \(\widehat{D_2}=\widehat{D_4}=65^0\) (đối đỉnh)
Vì a//b nên \(\widehat{C_4}=\widehat{D_2}=65^0\) (so le trong)
\(\widehat{C_3}+\widehat{C_4}=180^0\) (kề bù)
Hay \(\widehat{C_3}=180^0-65^0=115^0\)
PT
1
CM
15 tháng 8 2017
Cho hình vẽ:
a) Ta có a ⊥ c và b ⊥ c => a // b
b) Ta có: C ^ + D ^ = 180 0 (cặp góc kề bù)
D ^ = 180 0 − 55 0 = 125 0
W
15 tháng 3 2020
a) Xét tam giác ABC. Ta có:
Vì AD là tia phân giác của góc A nên:
\(\widehat{BAD}=\widehat{DAC}=\frac{\widehat{A}}{2}=40^{^o}\)
\(\widehat{ADB}=180^o-70^o-40^o=70^o\)
Vì \(\widehat{ADB}=\widehat{ABD}=70^o\)nên ABD là tam giác cân.
b)Vì \(\widehat{ADB}\)kề bù với \(\widehat{ADC}\)nên \(\widehat{ADC}=180^o-70^o=110^o\)
Do tam giác ACD là tam giác nên \(\widehat{ACD}=180^o-40^o-110^o=30^o\)
c) Đặt đỉnh ngoài của B là B1.
Ta có: \(\widehat{B_1}=180^o-70^o=110^o\)
8 tháng 1 2022
a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-80^0}{2}=50^0\)
b:\(\widehat{ABD}+\widehat{ABC}=180^0\)
\(\widehat{ACE}+\widehat{ACB}=180^0\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABD}=\widehat{ACE}\)
c: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
