PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QD
20 tháng 4 2017
Ta có : ˆA1A1^ và ˆA2A2^ là hai góc kề bù nên:
ˆA1+ˆA2=1800⇒ˆA2=1800−ˆA1=1800−1500=300A1^+A2^=1800⇒A2^=1800−A1^=1800−1500=300
Vì d1 // d2 và ˆA2A2^ so le trong với ˆB1B1^
⇒ˆB1=ˆA2=300⇒B1^=A2^=300
Vậy ˆB1=300
18 tháng 9 2017
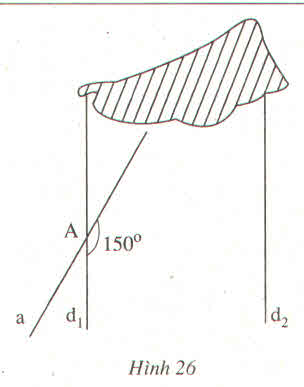
Gọi B giao điểm của a và d2.
d1 // d2 nên góc nhọn tại B bằng góc nhọn tại A và bằng
1800 - 1500= 300.
20 tháng 4 2017
a) Vẽ lại hình.
b) Ghi số đo ứng với các góc còn lại ta được hình bên:
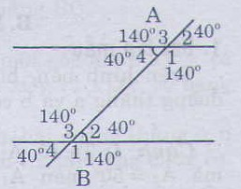
c) Ta có:
góc A4 + A1 = 180độ
=> góc A1 = 180 độ - 40 độ = 140 độ
=> góc A1 + góc B2= 40độ + 140 độ = 180 độ
Ý 2
Ta có:
góc B3 + góc B2 = 180 độ
=> góc B3 = 180 độ - 40 độ = 140 độ
=> góc A4 + B3 = 140 độ + 40 độ = 180 độ
QD
20 tháng 4 2017
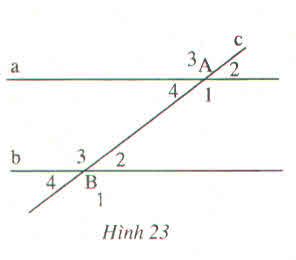
a) ˆB3B3^
b) ˆB2B2^
c) 1800 ; là cặp góc trong cùng phía
d) Bằng cặp góc so le trong ˆB2B2^=ˆA4A4^.
8 tháng 7 2017
a) \(\widehat{A_1}\)\(=\widehat{B_3}\)(vì là cặp góc so le trong)
b)\(\widehat{A_2}\)\(=\widehat{B_2}\)(vì là cặp góc đồng vị)
c)\(\widehat{B_3}\)\(+\widehat{A_4}\)\(=180^0\)(vì là cặp góc trong cùng phía)
d)\(\widehat{A_2}\)\(=\widehat{B_4}\)(vì là cặp góc cùng bằng \(\widehat{A_4}\) )
Ủng hộ mk nhé!!! ^.^
DH
13 tháng 6 2017
Vì \(b\ne d;b+d\ne0\) nên áp dụng tính chất cảu dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
Vậy \(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\) (đpcm)
Chúc bạn học tốt!!!
13 tháng 6 2017
Ta có:Nếu
\(\dfrac{a+c}{b+d}=\dfrac{a-c}{b-d}\)
thì \((a+c)(b-d)=(a-c)(b+d)\)
\(a(b-d)+c(b-d)=a(b+d)-c(b+d)\)
\(ab-ad+bc-cd=ab+ad-bc+cd\)
\(=\)\(ab-ab\)\(-ad+ad\)\(+bc-bc\)\(-cd+cd\)
\(=0\)
\(\Leftrightarrow\left(a+c\right)\left(b-d\right)\)\(=\left(a-c\right)\left(b+d\right)\)
\(\Leftrightarrow\dfrac{a+c}{b+d}\)\(=\dfrac{a-c}{b-d}\)
ngày mai tớ đi hok rùi
,huhu
23 tháng 9 2016
Ta có hình vẽ: m O n A B x y z m n a
Vẽ tia Oz nằm trong góc mOn sao cho Oz // Ax
Ta có: mAx = mOz = mo (đồng vị)
Lại có: mOz + zOn = mOn
=> mo + zOn = ao
=> zOn = no
Do zOn = yBn = no
Mà zOn và yBn là 2 góc đồng vị => Oz // By
Mặt khác, Oz // Ax
=> Ax // By (đpcm)
30 tháng 8 2017
a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
AH
Akai Haruma
Giáo viên
30 tháng 8 2017
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)
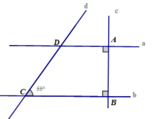
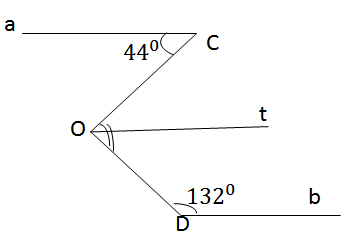
Cho hình vẽ:
a) Ta có a ⊥ c và b ⊥ c => a // b
b) Ta có: C ^ + D ^ = 180 0 (cặp góc kề bù)
D ^ = 180 0 − 55 0 = 125 0