Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do AMNP là hình vuông nên \(\widehat{QMB}=45^o\)
Lại có do C là điểm chính giữa của nửa đường tròn nên \(\widebat{CB}=90^o\Rightarrow\widehat{CMB}=45^o\)
(Góc nội tiếp)
Vậy thì \(\widehat{CMQ}=\widehat{CMB}+\widehat{BMQ}=45^o+45^o=90^o\)
Vậy CQ là đường kính hay C và Q đối xứng nhau qua O.
b) Ta thấyAMNP là hình vuông. MI là phân giác góc \(\widehat{AMB}\) nên \(\Delta MAI=\Delta MNI\left(c-g-c\right)\Rightarrow\widehat{MAI}=\widehat{MNI}\)
Lại có \(\widehat{MAI}=\widehat{IAM}\) nên \(\widehat{MNI}=\widehat{IAM}\)
Xét tứ giác AINB có \(\widehat{MNI}=\widehat{IAM}\) nên AINB là tứ giác nội tiếp (góc ngoài tại đỉnh bằng góc đối diện)

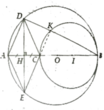
a, (O) và (I) tiếp xúc trong với nhau
b, Tứ giác ADCE là hình thoi
c, Có CK ⊥ AB, AD ⊥ DB
=> CK//AD mà CE//AD
=> B,K,D thẳng hàng
d, H K D ^ = H D K ^ ; I K B ^ = I B K ^
=> H K D ^ + I K B ^ = I B K ^ + H D K ^ = 90 0
=> I K H ^ = 90 0

1: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
2: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
góc EBC=1/2*sđ cung EC=90 độ
=>EB vuông góc BC
=>EB//OA
góc BCD=1/2*sđ cung BD=90 độ
=>CD vuông góc BC
=>CD//OA
=>góc AiF=góc CDF
=>góc AIF=góc ACF
=>AFIC nội tiếp
=>góc AIC=góc AFC=90 độ
góc AFC+góc EFC=90+90=180 độ
=>E,F,A thẳng hàng
a) Vì AB là đường kính \(\Rightarrow\angle ACB=90\Rightarrow AC\bot BC\)
mà \(ON\bot BC\) (N là điểm chính giữa cung BC)
\(\Rightarrow CK\parallel EN\) mà \(NK\bot KC\Rightarrow NK\bot EN\)
\(\Rightarrow\angle KCE=\angle KNE=\angle CEN=90\Rightarrow ECKN\) là hình chữ nhật
\(\angle KNO=90\Rightarrow KN\) là tiếp tuyến
b) ECKN là hình chữ nhật \(\Rightarrow ECKN\) cũng nội tiếp
\(\Rightarrow\angle KEN=\angle KCN=\angle CNE\) \((KC\parallel NE)\)
Vì \(AC\parallel ND\) mà ACND nội tiếp \(\Rightarrow ACND\) là hình thang cân
\(\Rightarrow\angle CNE=\angle ADN\Rightarrow\angle KEN=\angle ADN\) \(\Rightarrow KE \parallel AD\)
mà \(KA\parallel ED\) \(\Rightarrow KEDA\) là hình bình hành
c) Vì \(\left\{{}\begin{matrix}MO\bot AC\\NK\bot AC\end{matrix}\right.\) \(\Rightarrow MO\parallel NK\) \(\Rightarrow\dfrac{NI}{IM}=\dfrac{NK}{MO}\Rightarrow\dfrac{NI}{NK}=\dfrac{MI}{MO}=\dfrac{MI}{R}\)
Vì M,N lần lượt là điểm chính giữa cung AC,BC \(\Rightarrow\angle MON=90\)
\(\Rightarrow MN=\sqrt{OM^2+ON^2}=\sqrt{R^2+R^2}=\sqrt{2}R\)
Ta có: \(\dfrac{NI}{NK}+\dfrac{NI}{NO}=\dfrac{MI}{R}+\dfrac{NI}{R}=\dfrac{MI+NI}{R}=\dfrac{MN}{R}=\dfrac{\sqrt{2}R}{R}=\sqrt{2}\)
\(\Rightarrow NI\left(\dfrac{1}{NK}+\dfrac{1}{NO}\right)=\sqrt{2}\Rightarrow\dfrac{\sqrt{2}}{NI}=\dfrac{1}{NK}+\dfrac{1}{NO}\)
thank :3333