
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4a2b2 + 36a2b3 + 6ab4
= 2ab2(2a + 18ab + 3b2)
4a2b3 - 6a3b2
= 2a2b2(2b - 3a)


\(a.2a+4b+\left(-4b+5a\right)-\left(6a-9b\right)\)
\(=2a+4b-4b+5a-6a+9b\)
\(=\left(2a+5a-6a\right)+\left(4b-4b+9b\right)\)
\(=a+9b\)
\(b.6a\left[b+3a-\left(4a-b\right)\right]\)
\(=6a\left[b+3a-4a+b\right]\)
\(=6a\left[4a-a+b+b\right]\)
\(=6a\left(3a-2b\right)\)

6a - [ b + 3a - (4a - b)]
= 6a - [ b + 3a - 4a + b]
= 6a - [2b - a]
= 6a - 2b + a
= 7a - 2b

a, 4a^2b^3 - 6a^3b^2 = 2a^2b^2(2b - 3a)
b, 5(a + b) +x( a + b ) = ( 5 + x )( a + b )
c, (a - b)^2 - ( b - a ) = ( a - b )^2 + ( a - b ) = (a - b) ( a - b + 1)

\(\left(a+b\right)^4\)
\(=C^0_4\cdot a^4+C^1_4\cdot a^3b+C_4^2\cdot a^2b^2+C^3_4ab^3+C_4^4\cdot b^4\)
\(=a^4+4a^3b+6a^2b^2+4ab^3+b^4\)

\(7a\left(3a-5\right)+\left(2a-3\right)\left(4a+1\right)-\left(6a-2\right)^2\)
\(=21a^2-35a+8a^2+2a-12a-3-36a^2+24a-4\)
\(=-7a^2+4a-7\)

1) a^2 + b^2 + 2a - 2b - 2ab = (a^2 - 2ab + b^2) + (2a-2b) = (a-b)^2 + 2(a-b) = (a-b)(a-b+2)
2) 4a^2 - 4b^2 - 4a + 1 = ( 4a^2 - 4a +1) - 4b^2 = (2a-1)^2 - 4b^2 = (2a-1-2b)(2a-1+2b)
3) a^3+6a^2+12a+8= (a^3+8)+(6a^2+12a)= (a+2)(a^2-2a+4)+6a(a+2)=(a+2)(a^2-2a+4+6a)=(a+2)(a^2+4a+4)=(a+2)(a+2)^2=(a+2)^3
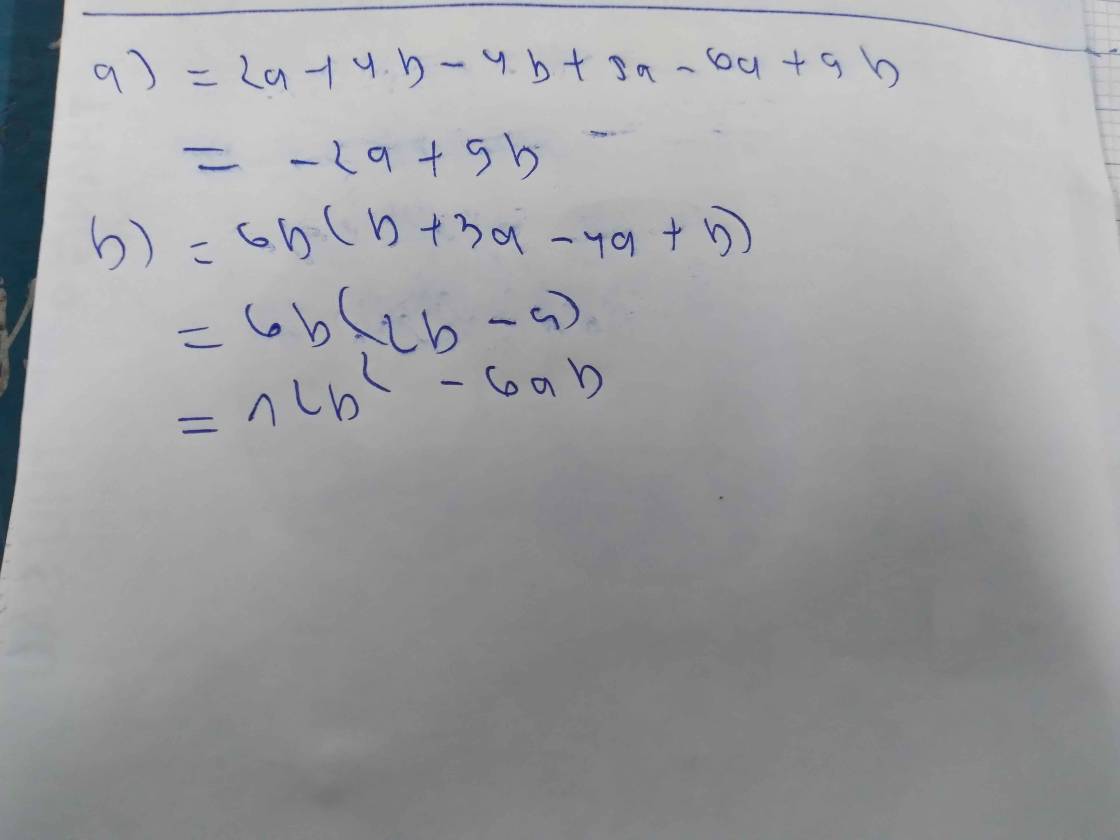
YC ĐỀ LÀ GÌ EM?
tính