K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 8 2019
\(\left(3x+1\right)^2+12x-\left(3x+5\right)^2+2\left(6x+3\right)\)
\(=9x^2+6x+1+12x-9x^2-30x-25+12x+6\)
\(=-18\)
Vậy đa thức trên ko phụ thuộc vào biến
N
4
TN
30 tháng 6 2016
A = ( 3x + 1 ) 2 + 12x - ( 3x + 5 ) 2+ 2( 6x + 3 )
=9x2+6x+1+12x-9x2-30x-25+12x+6
=(9x2-9x2)+(6x+12x-30x+12x)+1-25+6
=0+0+(-18)
=-18
30 tháng 6 2016
A=(3x+1)2+12x-(3x+5)2+2(6x+3)
=9x2+6x+1+12x-(9x2+30x+25)+12x+6
=9x2+6x+1+12x-9x2-30x-25+12x+6
=60x-18
\(\Rightarrow\)đề sai 100%
N
3
10 tháng 11 2019
\(\frac{12x^4-6x^3-9x^2}{-3x^2}-\left(2-3x\right)\left(2+3x\right)=-\left(3x+1\right)\)\(Dk:-3x^2\ne0\)\(< =>x\ne0\)
<=> \(-4x^2+2x+3-\left(2-3x\right).\left(2+3x\right)=-\left(3x+1\right)\)
<=> \(-4x^2+2x+3-4-6x+6x+9x^2=-3x-1\)
<=>\(5x^2+5x=0\)
<=> \(\orbr{\begin{cases}x=-1\left(n\right)\\x=0\left(l\right)\end{cases}}\)
CD
1
NH
0
HV
27 tháng 7 2023
chuyển vế sang r phân tích thành nhân tử, có thể dùng máy tính bỏ túi nhé bạn
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 7 2023
câu 1: 9\(x^2\) + 12\(x\) + 5 =11
(3\(x\))2 + 2.3.\(x\) .2 + 22 + 1 = 11
(3\(x\) + 2)2 = 11 - 1
(3\(x\) + 2)2 = 10
\(\left[{}\begin{matrix}3x+2=\sqrt{10}\\3x+2=-\sqrt{10}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=\sqrt{10}-2\\3x=-\sqrt{10}-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{10}-2}{3}\\x=\dfrac{-\sqrt{10}-2}{3}\end{matrix}\right.\)
Vậy S = {\(\dfrac{-\sqrt{10}-2}{3}\); \(\dfrac{\sqrt{10}-2}{3}\)}
Câu 2: 6\(x^2\) + 16\(x\) + 12 = 2\(x^2\)
6\(x^2\) + 16\(x\) + 12 - 2\(x^2\) = 0
4\(x^2\) + 16\(x\) + 12 = 0
(2\(x\))2 + 2.2.\(x\).4 + 16 - 4 = 0
(2\(x\) + 4)2 = 4
\(\left[{}\begin{matrix}2x+4=2\\2x+4=-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=-2\\2x=-6\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)
S = { -3; -1}
3, 16\(x^2\) + 22\(x\) + 11 = 6\(x\) + 5
16\(x^2\) + 22\(x\) - 6\(x\) + 11 - 5 = 0
16\(x^2\) + 16\(x\) + 6 = 0
(4\(x\))2 + 2.4.\(x\) . 2 + 22 + 2 = 0
(4\(x\) + 2)2 + 2 = 0 (1)
Vì (4\(x\)+ 2)2 ≥ 0 ∀ ⇒ (4\(x\) + 2)2 + 2 > 0 ∀ \(x\) vậy (1) Vô nghiệm
S = \(\varnothing\)
Câu 4. 12\(x^2\) + 20\(x\) + 10 = 3\(x^2\) - 4\(x\)
12\(x^2\) + 20\(x\) + 10 - 3\(x^2\) + 4\(x\) = 0
9\(x^2\) + 24\(x\) + 10 = 0
(3\(x\))2 + 2.3.\(x\).4 + 16 - 6 = 0
(3\(x\) + 4)2 = 6
\(\left[{}\begin{matrix}3x+4=\sqrt{6}\\3x+4=-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}3x=-4+\sqrt{6}\\3x=-4-\sqrt{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}-4}{3}\\x=-\dfrac{\sqrt{6}+4}{3}\end{matrix}\right.\)
S = {\(\dfrac{-\sqrt{6}-4}{3}\); \(\dfrac{\sqrt{6}-4}{3}\)}
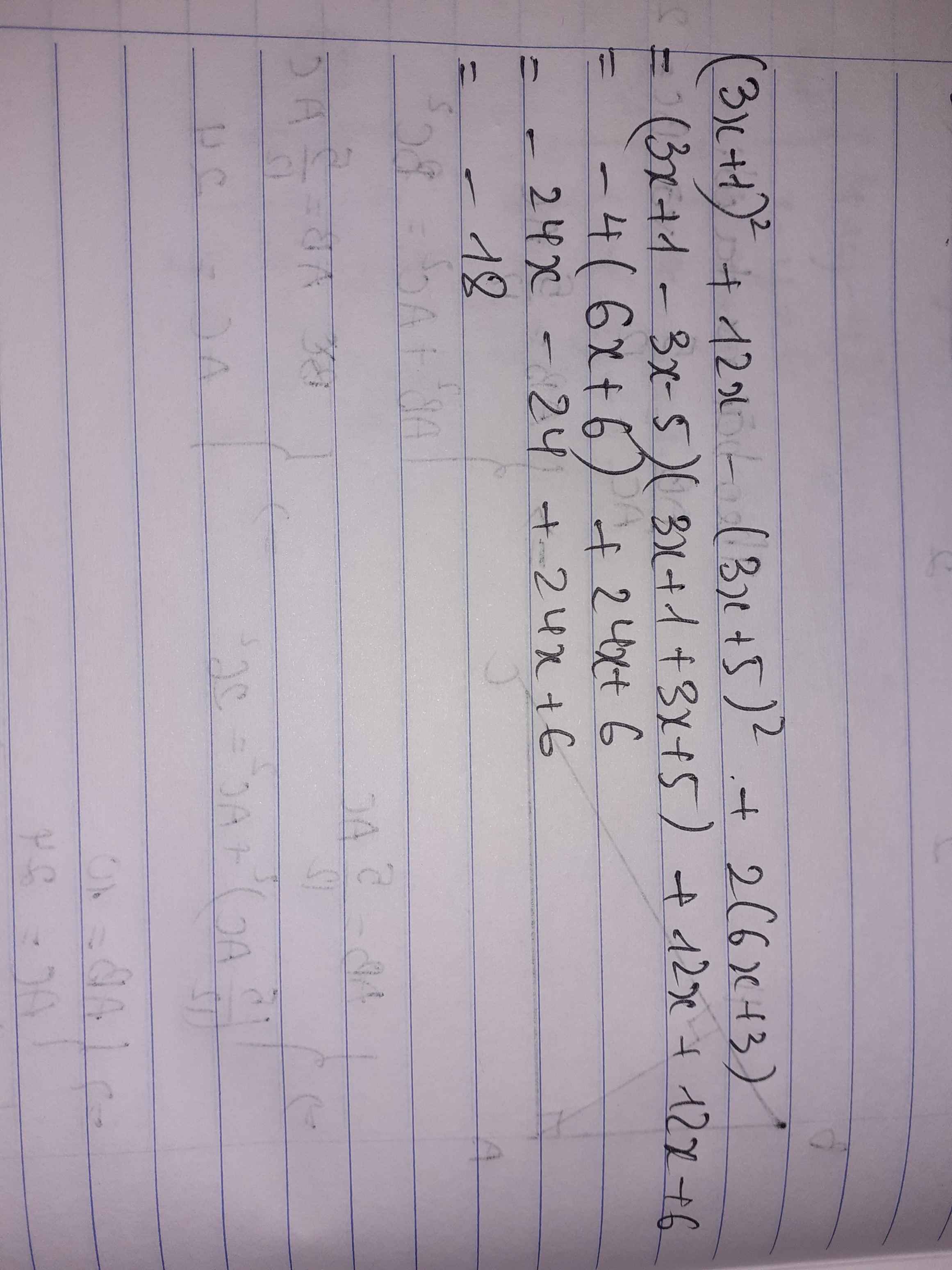
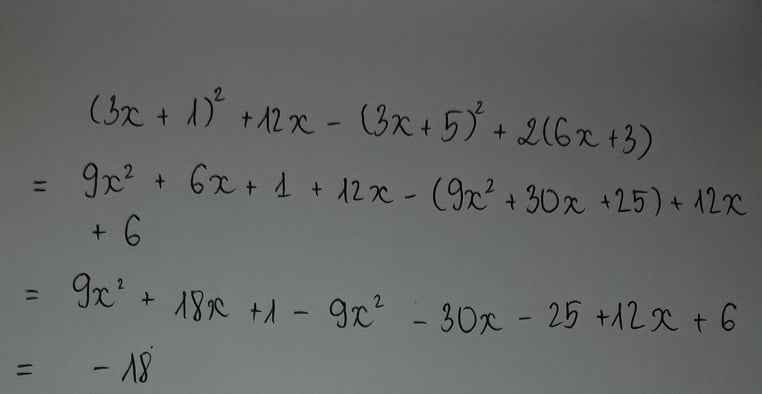
cm bieu thuc k phu thuoc vao bien x