KT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KT
2
23 tháng 10 2017
cứ sai nhỉ. đề bài thật này các bạn ơi
1 ô tô xuất phát từ A đến B, trên 1/2quãng đường đầu đi với vận tốc v1, 1/2 quãng đường sau đi với vận tốc v2. 1 ô tô khác xuất phát từ B đến A, trong 1212 thời gian đầu đi với vận tốc v1 và trong 1/2 thời gian sau đi với vận tốc v2. Biết v1 = 20km/h, v2 = 60km/h. Nếu xe đi từ B xuất phát muộn hon 30 phút so với xe đi từ A thì 2 xe dến địa điểm đã định cùng lúc. Nếu 2 xe cùng xuất phát và đi vói vận tốc TB của chúng thì 2 chúng sẽ gặp nhau tại vị trí cách A bao xa?
30 tháng 7 2016
ta có:
v1-v2=10
\(\Rightarrow v_1=v_2+10\left(1\right)\)
mà ô tô 1 đến trước ô tô 2 1h nên:
t2-t1=1
\(\Leftrightarrow\frac{S}{v_2}-\frac{S}{v_1}=1\)
\(\Leftrightarrow\frac{300}{v_2}-\frac{300}{v_1}=1\)
thế (1) vào phương trình trên ta có:
\(\frac{300}{v_2}-\frac{300}{v_2+10}=1\)
\(\Rightarrow v_2=50\)
\(\Rightarrow v_1=60\)
29 tháng 7 2016
Gọi v1 và v2 là vận tốc của hai ô tô.
Ta có : v1 - v2 = 10 => v1 = v2 + 10
=> t2 = t1 + 1 => t1 = t2 - 1
Ta có Phương trình:
v1 . t1 = v2 . t2
<=> (v2 + 10) (t2 - 1) = v2 . t2
<=> S2 = 10t2 -1v2 - 4 = S2
<=> 10t2 = 1v2 = 4
Mặc khác :
v2 . t2 = 300 (km)
<=> t2 = 300 : v2
Thế vào phương trình :
3000 : v2 - 0,4 v2 = 4
=> v2 = 40
=> v1 = 50
M
0
C
0
TD
19 tháng 7 2021
giải
*Hằng ngày
Quãng đường xe 1 đi
S1=V1.(9-6)=3v1
quãng đường xe 2
S2=v2(3-(7-6))=2v2
ta có
S1+S2=AB\(\leftrightarrow\)3v1+2v2=AB (1)
*Hôm khác
quãng đg xe 1 đi
S3=(9,8-8)V1=1,8V1
quãng đường xe 2
S4=(1,8+(8-7))V2=2,8V2
ta có: S1+S2=AB\(\leftrightarrow\)1,8V1+2,8V2=AB (2)
Từ (1),(2) \(\Rightarrow\)3V1+2V2=1,8V1+2,8V2
\(\Rightarrow\)\(\left\{{}\begin{matrix}V1=\dfrac{2}{3}V2\\V2=1,5V1\end{matrix}\right.\)
Thời gian xe 1 đi từ A đến B
t1=\(\dfrac{AB}{V1}\)=\(\dfrac{3V1+2V2}{V1}\)=\(\dfrac{3V1+2.1,5V1}{V1}\)=6(h)
T/g xe 2 đi
t2=....=4(h)
Vậy hằng ngày xe 1 đi đến B lúc 6+6=12h
xe 2 đi đến A lúc 7+4=11h
H9
HT.Phong (9A5)
CTVHS
13 tháng 5 2023
Thời gian đi của ô tô thứ nhất:
\(t_1=\dfrac{s}{2v_1}+\dfrac{s}{2v_2}=\dfrac{s\left(v_1+v_2\right)}{2v_1v_2}\)
Vận tốc trung bình của ô tô thứ nhất:
\(v_{tbA}=\dfrac{s}{t}=\dfrac{2v_1v_2}{v_1+v_2}=\dfrac{2.20.60}{20+60}=30km/h\)
Theo đề ta có: \(s=\dfrac{t_2}{2}v_1+\dfrac{t_2}{2}v_2=t_2\left(\dfrac{v_1+v_2}{2}\right)\)
Vận tốc trung bình của ô tô thứ hai:
\(v_{tbB}=\dfrac{s}{t_2}=\dfrac{v_1+v_2}{2}=\dfrac{20+60}{2}=40km/h\)
Theo đề bài ta có: \(\dfrac{s}{v_A}-\dfrac{s}{v_B}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{s}{30}-\dfrac{s}{40}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{4s}{120}-\dfrac{3s}{120}=\dfrac{60}{120}\)
\(\Leftrightarrow s=60\left(km\right)\)
Vậy hai xe xuất phát cùng lúc sẽ gặp nhau sau:
\(s_1+s_2=s_{AB}\)
\(\Leftrightarrow30t+40t=60\)
\(\Leftrightarrow70t=60\)
\(\Leftrightarrow t=\dfrac{60}{70}\approx0,9\left(h\right)\)
Hai xe gặp nhau tại điểm cách điểm A:
\(s_1=v_A.t=30.0,9=27\left(km\right)\)
H9
HT.Phong (9A5)
CTVHS
2 tháng 4 2023
Thời gian xe A chạy trên nữa quãng đường đầu:
\(t_1=\dfrac{\dfrac{s_{AB}}{2}}{\upsilon_1}=\dfrac{\dfrac{s_{AB}}{2}}{20}=\dfrac{s_{AB}}{2.20}=\dfrac{s_{AB}}{40}\left(h\right)\)
Thời gian xe A chạy trên nữa quãng đường sau:
\(t_2=\dfrac{\dfrac{s_{AB}}{2}}{\upsilon_2}=\dfrac{\dfrac{s_{AB}}{s}}{60}=\dfrac{s_{AB}}{2.60}=\dfrac{s_{AB}}{120}\left(h\right)\)
Vận tốc trung bình của xe A trên cả quãng đường AB:
\(\upsilon_{tbA}=\dfrac{\dfrac{s_{AB}}{2}+\dfrac{s_{AB}}{2}}{\dfrac{s_{AB}}{40}+\dfrac{s_{AB}}{120}}=\dfrac{s_{AB}}{\dfrac{s_{AB}}{40}+\dfrac{s_{AB}}{120}}=\dfrac{s_{AB}}{\dfrac{s_{AB}}{30}}=30\left(km/h\right)\)
Quãng đường mà xe B đi được trong nữa thời gian đầu:
\(s_1=\upsilon_1.\dfrac{t}{2}=20.\dfrac{t}{2}=10t\left(km\right)\)
Quãng đường xe B đi được trong nữa thời gian sau:
\(s_2=\upsilon_2.\dfrac{t}{2}=60.\dfrac{t}{2}=30t\left(km\right)\)
Vận tốc trung bình của xe B trên cả quãng đường AB:
\(\upsilon_{tbB}=\dfrac{s_1+s_2}{\dfrac{t}{2}+\dfrac{t}{2}}=\dfrac{10t+30t}{t}=\dfrac{40t}{t}=40\left(km/h\right)\)
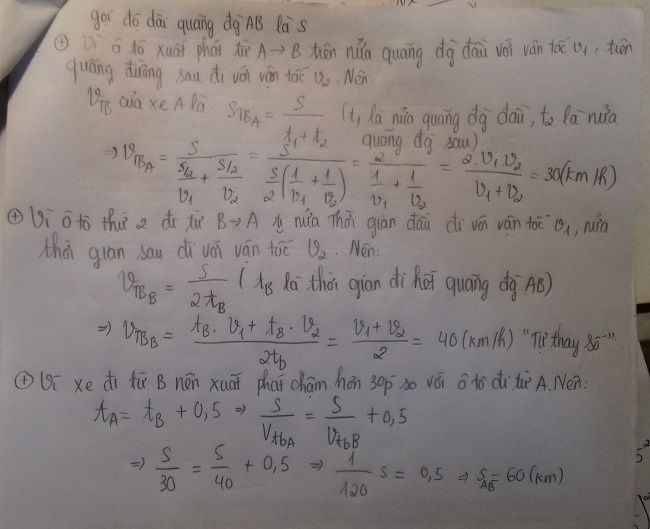
???????? k thể ns ak pn