Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
Gọi số nữ và số nam thuận tay trái lần lượt là x(người) và y(người).
Khi đó, do tổng số người thuận tay trái là 10 người nên ta có
x+y=10
Lại có số nữ thuận tay phải gấp 3 lần số nữ thuận tay trái nên số nữ thuận tay phải là 3x(người). Số nam thuận tay phải gấp 5 lần số nam thuận tay trái nên số nam thuận tay phải là 5y(người).
Lại có tổng số người thuận tay phải là 44 nên ta có :
\(3x+5y=44\)
Vậy ta có hệ
\(\hept{\begin{cases}x+y=10\\3x+5y=44\end{cases}}\)
Suy ra \(x=3,y=7\)
Vậy có 3 nữ thuận tay trái, 7 nam thuận tay trái.
Bài 2 :
\(\hept{\begin{cases}a^2+b^2+c^2=27\left(1\right)\\a+b+c=9\left(2\right)\end{cases}}\)
Áp dụng bất đẳng thức Cô si ta có :
\(2\left(a^2+b^2+c^2\right)=\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\)
\(\ge2ab+2bc+2ca\)
\(\Rightarrow a^2+b^2+c^2\ge ab+bc+ca\)
Dấu " = " xảy ra <=> a=b=c
\(\left(2\right)\Leftrightarrow\left(a+b+c\right)^2=81\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=81\)
\(\Rightarrow81\le a^2+b^2+c^2+2\left(a^2+b^2+c^2\right)=3\left(a^2+b^2+c^2\right)\)
\(\Rightarrow27\le a^2+b^2+c^2\left(3\right)\)
Từ (1) và (3) => dấu " = " xảy ra => a=b=c=3
\(\Rightarrow B=\left(3-4\right)^{2018}+\left(3-4\right)^{2019}+\left(3-4\right)^{2020}\)
\(=1-1+1=1\)

gọi số cần tìm là ab
theo bài ra ta có
ab x 36 = 2ab2
ab x 36 =2000+ ab x 10 +2
ab x 36 - ab x 10= 2000+2
abx 26=2002
ab = 2002 : 26 = 77
vậy số cần tìm là 77
các bạn cho mình vài li-ke cho tròn 450 với

Gọi số cần tìm là bcde số viết thêm vào bên trái là a. theo đề bài
=> abcde8=34.bcde => 100000a+10.bcde+8=34.bcde => 100000a+8=24.bcde => 12500a+1=3.bcde (*) => 12498a+2a+1=3.bcde
Ta thấy 3.bcde chia hết cho 3 => 12498a+2a+1 cũng phải chia hết cho 3 mà 12498a chia hết cho 3 nên 2a+1 phải chia hết cho 3
=> 2a+1={3; 6; 9; 12; 15; 18} => 2a = {2; 5; 8; 11; 14; 17} . Do 2a chẵn => 2a={2; 8; 14} => a={1; 4; 7}
Thay các giá trị của a vào (*) => bcde rồi thử lại để chon kq thỏa mãn dk đề bài

Ta thấy trên 90 số được tạo có tính chất. Tổng 2 số cách đều 2 biên (1001 và 9999) là 11 000
| 1001 | 1111 | 1221 | 1331 | ……. |
+ | 9999 | 9889 | 9779 | 9669 | …… |
| 11000 | 11000 | 11000 | 11000 | ……. |
Nên tổng của 90 số đó là: 11 000 x 90 : 2 = 495 000

Có 7 bạn nói câu “Đa số chúng ta là con trai” và 6 bạn nói “Đa số chúng ta là con gái”. Do đó sẽ có ít nhất 6 cặp khác giới kề nhau, nhưng cũng có ít nhất 6 cặp cùng giới kề nhau.
Hai người kề nhau nói các mệnh đề khác nhau, trừ bạn đầu tiên và bạn cuối cùng. Ta thấy trừ các vị trí 13, 1, 2, ở các vị trí khác, không thể có 3 người cùng giới kề nhau, vì ví dụ nếu có Nam 1, Nam 2, Nam 3 kề nhau thì Nam 1 và Nam 2 nói ngược nhau, mặc dù về nguyên tắc họ phải nó thật.
Vì phải có ít nhất 6 cặp cùng giới kề nhau nên từ đây suy ra cách sắp duy nhất thỏa mãn yêu cầu là Nam, Nam, Nữ, Nữ, Nam, Nam, Nữ, Nữ, Nam, Nam, Nữ, Nữ, Nam.
Vậy có 7 bạn trai ngồi quanh bàn.
duyệt đi
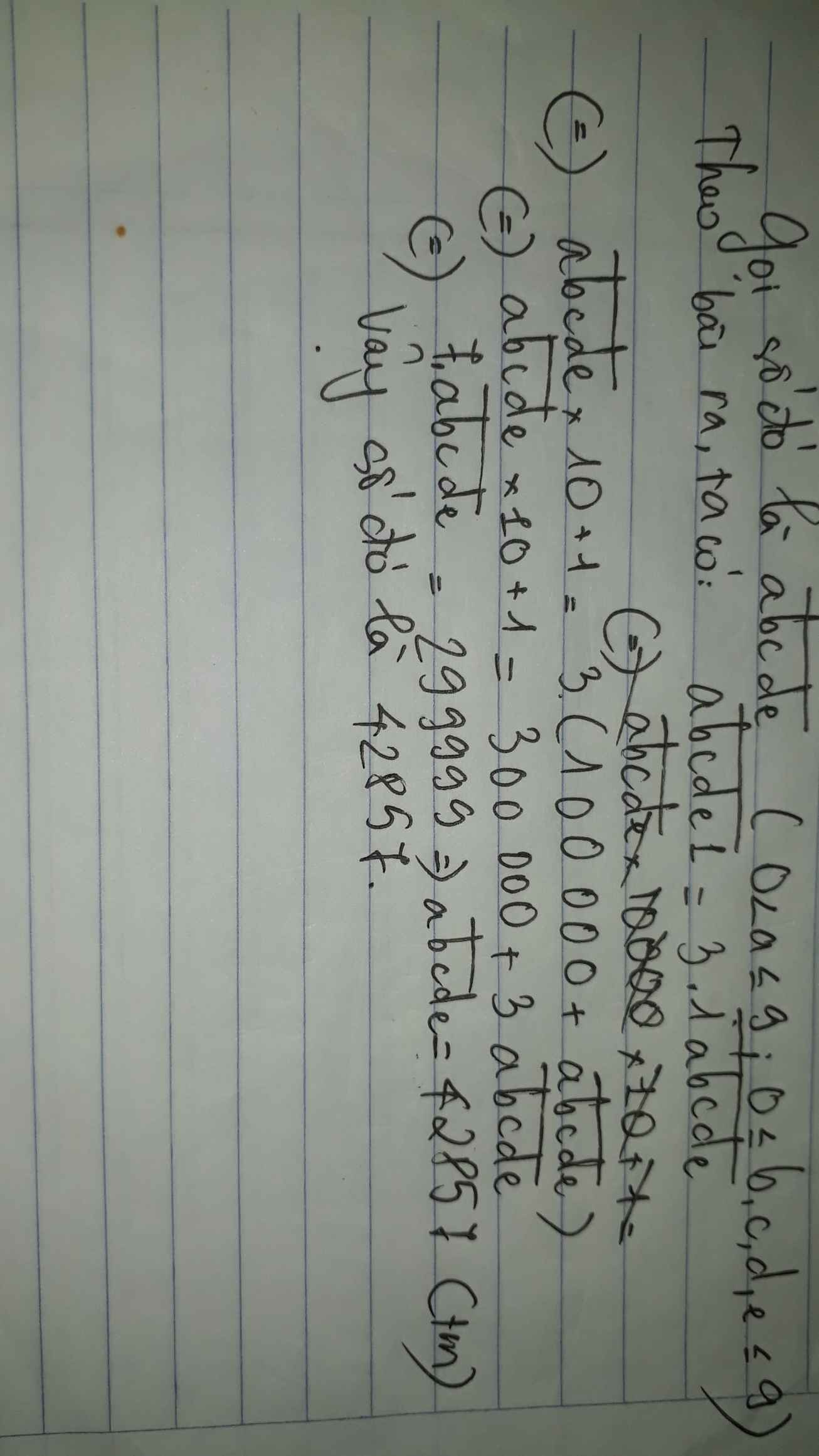
Gọi: số vận động viên nữ thuận tay trái là x ( người ) ( x > 0 )
số vận động viên nam thuận tay trái là y ( người ) ( y > 0 )
Khi đó:
số vận động viên nữ thuận tay phải là 5x ( người )
số vận động viên nam thuận phải là 9x ( người )
Đội bóng bàn đó có 18 người thuận tay trái và 122 người thuận tay phải nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=18\\5x+9y=122\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9x+9y=162\\5x+9y=122\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=40\\x+y=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=8\end{matrix}\right.\)
Vậy số vận động viên nữ là: 10 + 5\(\times\)10 \(=\) 60 (vận động viên)
số vận động viên nam là : 8 + 9\(\times\)8 \(=\) 80 (vận động viên)
\(=\)\(\times\)\(\times\)